0.前言
前面几篇文章讲了水晶球的安装和基本用法，这篇文章通过一个案例来简单介绍一下具体用法
本文用的excel测试数据下载地址：
链接: https://pan.baidu.com/s/1TgsC46Bn3WlmTGuQgNhlCg?pwd=7emb 提取码: 7emb
1.问题描述
一个报童卖报，每份报纸成本费用1.5,售价2.5，如果退回的话每份退0.5。然后每天的销售额在40—70之间。目标就是利润最大化。
2.模型建立
我们把上面的数据转化成模型
其中需求数量是模拟需求数量四舍五入的结果。
销售收入=单价*min(订单数量，需求数量)
购买价格=成本*订单数量
残值=退回成本-MAX(订单数量-需求数量，0)
利润=销售收入-购买价格+残值
一、基础用法
1.定义假设单元格
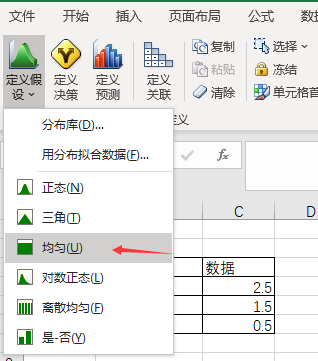
本样例中一个随机输入单元格是模拟需求数量C15。我们在excel中选中C15，然后点击“定义假设”，选中一种数据分布方式，本文选的是均匀分布，点击确定。
我们将定义假设的范围填入，点击“确定”按钮，定义假设单元格就设定完毕。
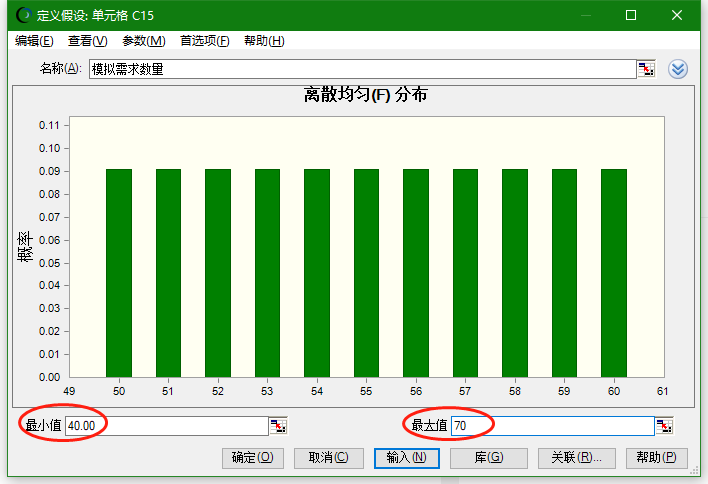
2.定义预测单元格
计算机模拟的电子表格模型并没有包括单元格，但是预测单元格可以实现这一个作用。在本样例中选中的是“利润”C25单元格，我们选中后，点击“定义预测”，把名称和单位填上(这里的名称和单位是为了后面出图用的)。
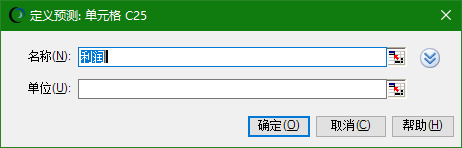
点击确定后，利润单元格就变色了。
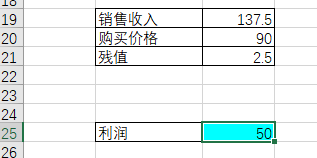
3.设定运行参数并运行
我们在实验次数那个地方设置运行参数，然后点击启动，然后就会产生下面的图形
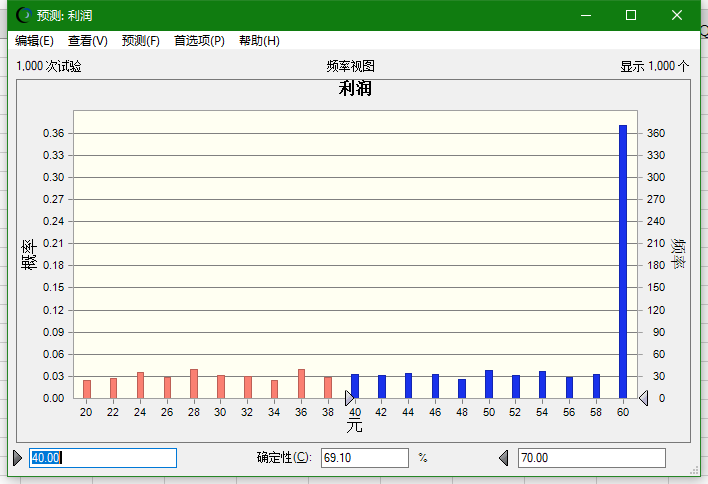
可以看出，在1000次实验中，订购数量为60份出现的次数最多，从侧面说明60份这个数量是一个比较合理的值。
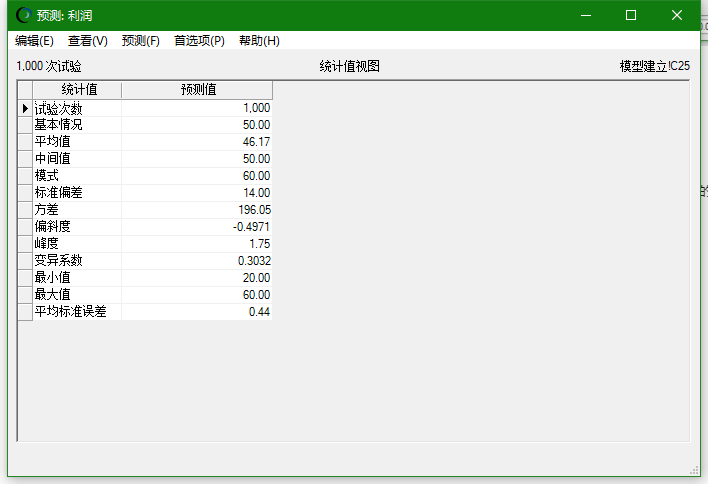
当然，你也可以点击“查看”里面的“统计值”来查看更详细的数据。
二、用决策表制定决策
1.决策变量
我们可以用决策表制定决策：在本样例中，在40到70之间的哪个订购量能够最大化每天的平均利润呢？
当然这个也可以反过来想，你要达到某个利润，然后反推决策变量应该制定为多少合适。
在本例中，我们选中需要的决策变量，也就是C11，然后点击“定义决策”
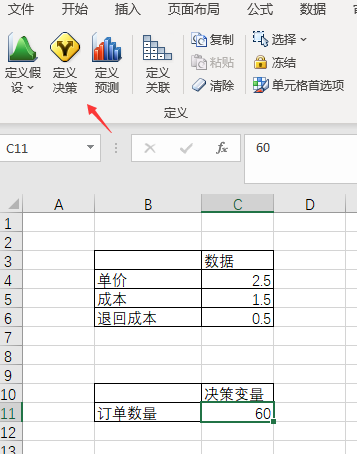
我们把上限和下限全部填入，点击“确定”即可。
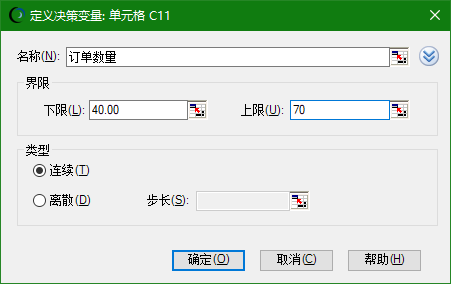
这个时候决策变量就变黄了
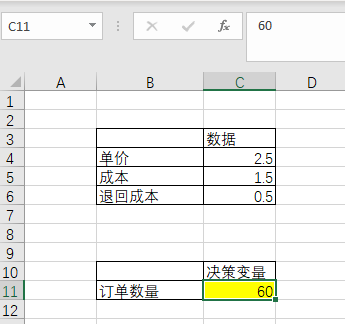
2.利用OptQuest做决策
上面我们用了模拟统计的方法，得出的结论是60，我们打开OptQuest， 看出默认是没有的，这个工具是根据目标和要求得出一个比较合适的结论。
然后我们制定了决策变量，下面就可以用QotQuest做决策分析了。
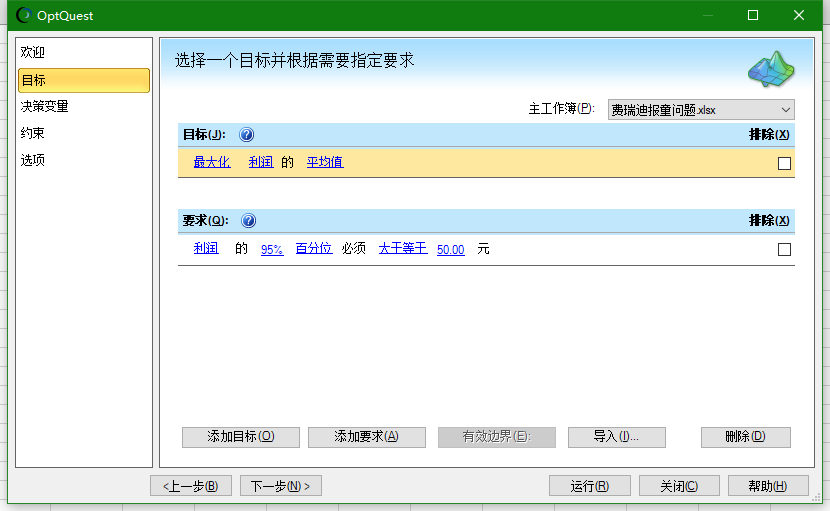
目标指的是 整个计划要达到一个什么程度，比如这个项目就是让利润最大化。
要求就是一些简单的限制或者输入条件，在这个地方我们可以让要求是利润达到100元能否实现。
目标和要求都应该是定义预测的部分。
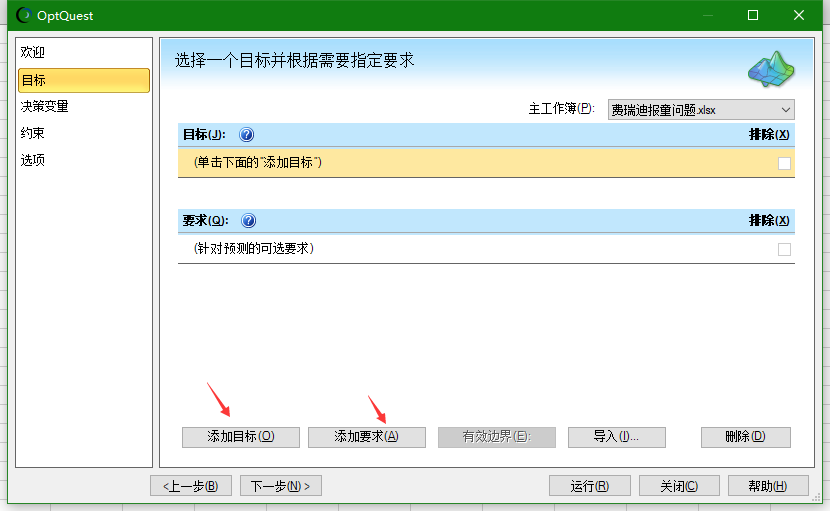
然后修改完后点击运行，看一下结论。
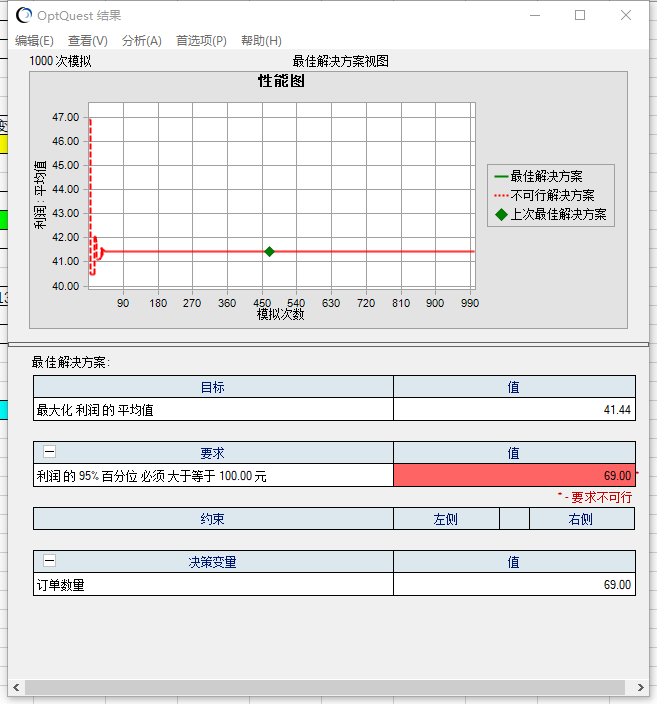
根据结论，我们可以看出，在此项目中加入[40,70]这个约束条件的情况下， 让利润达到100元是不可能实现的，那么可以考虑将利润缩减一下看能否实现。
继续预测。。。。。
给出的结论是
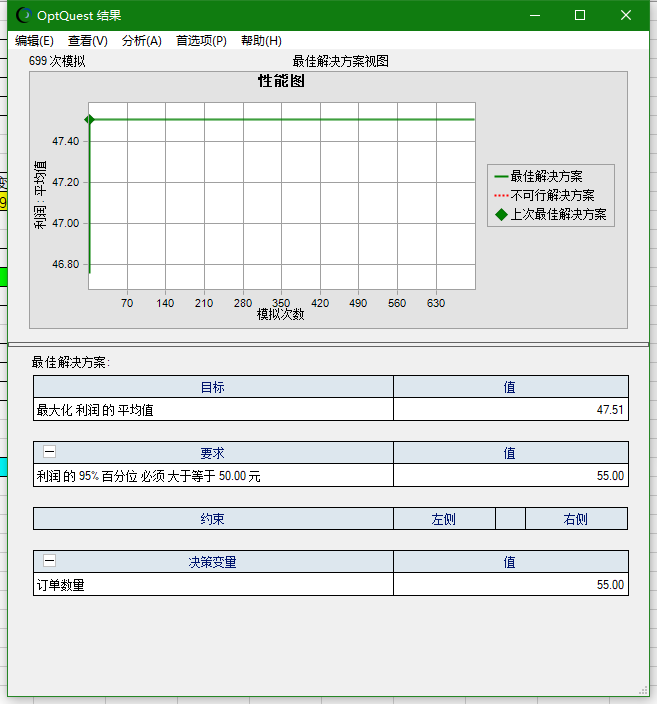
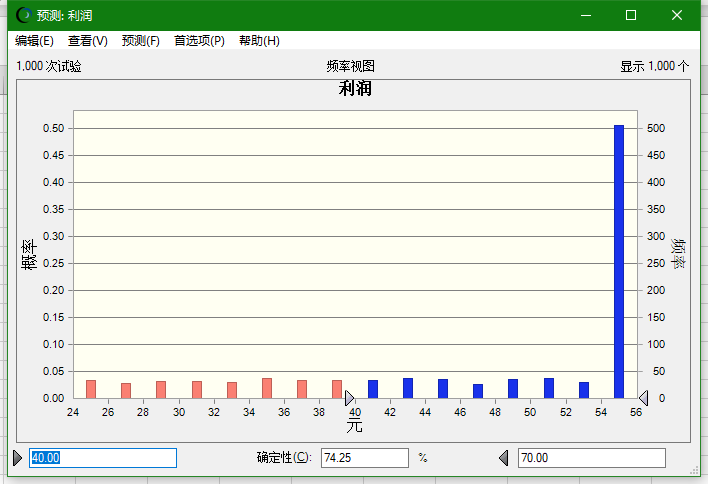
对于上面这个结论可以这样来解释：在1000次实验中，最大化利润的平均值是47.51。对于我们的输入要求”利润的95%百分位大于等于50.00元“ ，意为当决策变量（订单数量）为55时，”在95%的情况下可以达到利润大于等于50“， 这件事情发生的概率只有74.25% 。
返回目录：其他