【题目描述】
八皇后问题是一个古老而著名的问题,是回溯算法的典型例题。该问题是十九世纪著名的数学家高斯1850年提出:在8X8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线(对角线)上,问有多少种摆法。
【输入描述】
无
【输出描述】
一共有多少种摆法
【样例输入】
无
【样例输出】
92
【题目分析】
(1)框架分析
放置第i个(行)皇后的算法为:
int search(i);
{
int j;
for (第i个皇后的位置j=1;j<=8;j++ ) //在本行的8列中去试
if (本行本列允许放置皇后)
{
放置第i个皇后;
对放置皇后的位置进行标记;
if (i==8) 输出 //已经放完个皇后
else search(i+1); //放置第i+1个皇后
对放置皇后的位置释放标记,尝试下一个位置是否可行;
}
}(2)
主要解决几个问题:
冲突:包括行、列、两条对角线
行:规定每行放一个皇后,不会造成行上的冲突
列:当第col列被某个皇后占领后,则同一列上所有位置不在放皇后,要把
flag[col] 置为被占领状态。
对角线:对角线有两个方向。当第n行第col列皇后占领后,上下对角线标记
为被占领状态。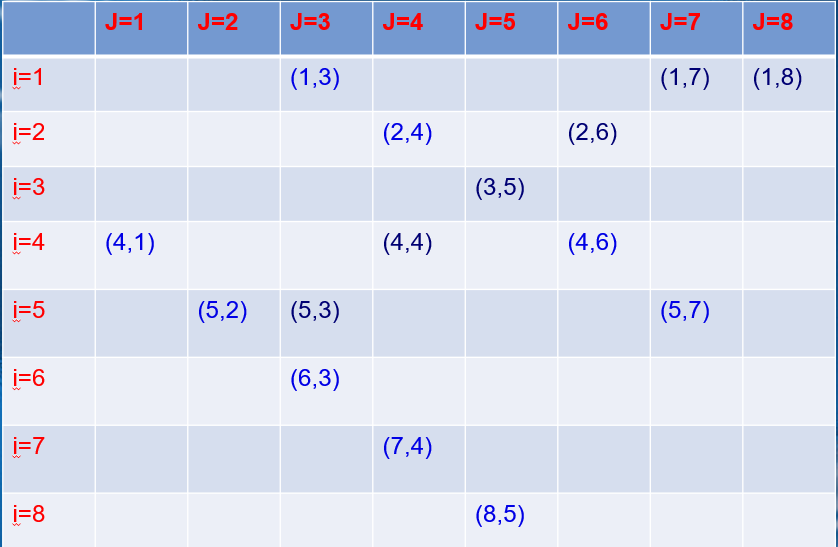
规律:左上到右下,我们叫主对角线,同一主对角线i-j是个常数。右上到左下,我们称为副对角线,同一副对角线i+j是个常数。所以,
左上到右下: i-j+7 (C++ 不支持负数)
右上到左上: i+j
(3)
1.初始化(清除棋盘)
2.循环8次
放置一个皇后;
检查是否满足条件,如满足,登记皇后位置;
如不满足,则退回,增加一步后在放皇后。
3. 知道放置最后一个皇后
【参考代码1】
用col表示列,L_diagonal表示主对角线(就是左上到右下),R_diagonal表示副对角线(就是右上到左下)
#include<iostream>
using namespace std;
int col[10],L_diagonal[10],R_diagonal[10]; //分别表示标记数组,列数组,主对角线数组,副对角线数组
int ans[10]; //结果数组
int sum;
int dfs(int i)//用i来表示皇后所处的行位置
{
int j; //用j表示皇后所处的列位置
for(j=1;j<=8;j++)
if((col[j]==0)&&(L_diagonal[i-j+7]==0)&& (R_diagonal[i+j]==0))// 列、主对角线、副对角线没有被占领过
{
ans[i]=j; //在当前(i,j)位置上摆放一个皇后
col[j]=1; //占领当前(i,j)所在的列
L_diagonal[i-j+7]=1; //占领当前(i,j)所在的主对角线
R_diagonal[i+j]=1; //占领当前(i,j)所在的副对角线
if(i==8)
{
//print(); //此题没有要求输出
sum++; //摆放种数加1
}
else
dfs(i+1);
col[j]=0; //回溯(i,j)所在的列
L_diagonal[i-j+7]=0; //回溯当前(i,j)所在的主对角线
R_diagonal[i+j]=0;//回溯当前(i,j)所在的副对角线
}
}
int main()
{
dfs(1);
cout<<sum<<endl;
return 0;
}
返回目录:题解目录