一、单项选择题(共 20 题,每题 1.5 分,共计 30 分。每题有且仅有一个正确选项。)
1、在二进制下,1101001 + ( B ) = 1110110。
A、1011 B、1101 C、1010 D、1111
【分析】题目比较简单,
1101001
0001101
———–
1110110
2、字符“0”的 ASCII 码为 48,则字符“9”的 ASCII 码为( B )。
A、39 B、57 C、120 D、视具体的计算机而定
【分析】48+9=57
3、一片容量为 8GB 的 SD 卡能存储大约( C )张大小为 2MB 的数码照片。
A、1600 B、2000 C、4000 D、16000
【分析】8GB=8*1024/2 = 4096(张)
4、摩尔定律(Moore’s law)是由英特尔创始人之一戈登·摩尔(Gordon Moore)提出来的。根据摩尔定律,在过去几十年以及在可预测的未来几年,单块集成电路的集成度大约每( C )个月翻一番。
A、1 B、6 C、18 D、36
【分析】摩尔同学说 18~24月翻一番
5、无向完全图是图中每对顶点之间都恰有一条边的简单图。已知无向完全图 G 有 7 个顶点,则它共有( B )条边。
A、7 B、21 C、42 D、49
【分析】
完全图的边的公式
$\frac{n(n-1)}{2}$
n表示顶点,带入得21。
6、寄存器是(D )的重要组成部分。
A、硬盘 B、高速缓存 C、内存 D、中央处理器(CPU)
【分析】
CPU由运算器、控制器、寄存器三部分构成。
7、如果根结点的深度记为 1,则一棵恰有 2011 个叶结点的二叉树的深度最少是( C )。
A、10 B、11 C、12 D、13
【分析】叶子结点2011个,总结点大概是叶子结点的两倍,也就是4022个。
根据公式$2^{k}-1<=4022$ k=11,题目中说的根节点深度为1,所以答案是12。
8、体育课的铃声响了,同学们都陆续地奔向操场,按老师的要求从高到矮站成一排。每个同学按顺序来到操场时,都从排尾走向排头,找到第一个比自己高的同学,并站在他的后面。这种站队的方法类似于( B )算法。
A、快速排序 B、插入排序 C、冒泡排序 D、归并排序
【分析】
题目中描述的是插入排序。A选项快速排序用到的是分治法,每次分为左右两个区间。C选项是两两比较。D选项是先分组再比较再合并。
9、一个正整数在二进制下有 100 位,则它在十六进制下有( 25 )位。
A、7 B、13 C、25 D、不能确定
【分析】
二进制转十六进制是每四位二进制转换成一位十六进制,所以100/4=25
10、有人认为,在个人电脑送修前,将文件放入回收站中就是已经将其删除了。这种想法是( C )。
A、正确的,将文件放入回收站意味着彻底删除、无法恢复
B、不正确的,只有将回收站清空后,才意味着彻底删除、无法恢复
C、不正确的,即使将回收站清空,文件只是被标记为删除,仍可能通过恢复软件找回
D、不正确的,只要在硬盘上出现过的文件,永远不可能被彻底删除
【分析】
不论是把文件删除到回收站,然后清空回收站,还是不经过回收站直接删除,都存在被恢复的可能。数据进行恢复与硬盘本身的结构有关系,硬盘之所以能储存数据,是因为其盘片上有凹凸不平的存储介质,相当于人大脑的记忆细胞,把写入硬盘的数据记忆下来以供读取。当我们把硬盘格式化后,这些存储介质并没有被抹平;只是改变了它的逻辑地址而已,当有新的数据写入的时候,它才会被覆盖掉,数据恢复软件也正是基于这一原理,突破操作系统的寻址和编址方式,把尚未被覆盖的数据收集起来保存到新的位置。
11、广度优先搜索时,需要用到的数据结构是( B )。
A、链表 B、队列 C、栈 D、散列表
【分析】
队列这种数据结构是广度优先搜索算法优先选择的数据结构。第一是因为队列的存储机制为先进先出,而广度优先搜索算法恰好需要保证优先访问已访问顶点的未访问邻接点。因此队列最适合广度优先算法的存储法则。
12、在使用高级语言编写程序时,一般提到的“空间复杂度”中的“空间”是指(A )。
A、程序运行时理论上所占的内存空间
B、程序运行时理论上所占的数组空间
C、程序运行时理论上所占的硬盘空间
D、程序源文件理论上所占的硬盘空间
【分析】程序运行时都是先在内存上运行。
13、在含有 n 个元素的双向链表中查询是否存在关键字为 k 的元素,最坏情况下运行的时间复杂度是( )。
A、O(1) B、O(log n) C、O(n) D、O(n log n)
【分析】
n个元素查找k,最坏的情况就是最后一个才找到k。在这种情况下,时间复杂度是O(n)
14、生物特征识别,是利用人体本身的生物特征进行身份认证的一种技术。目前,指纹识别、虹膜识别、人脸识别等技术已广泛应用于政府、银行、安全防卫等领域。以下不属于生物特征识别技术及其应用的是( C )。
【分析】
C选项密码验证只是数字识别,没有用到指纹,不属于生物特征识别。
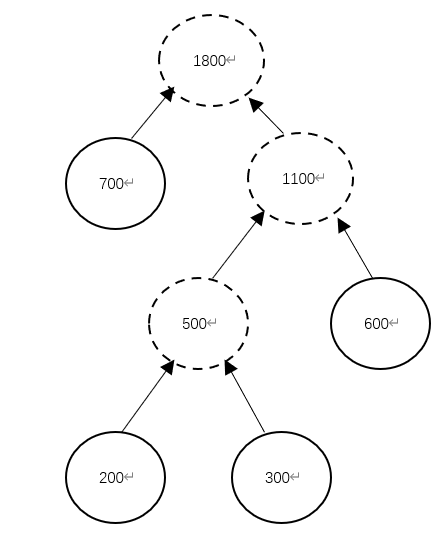
15、现有一段文言文,要通过二进制哈夫曼编码进行压缩。简单起见,假设这段文言文只由 4 个汉字“之”、“乎”、“者”、“也”组成,它们出现的次数分别为 700、600、300、 200。那么,“也”字的编码长度是(C )。
A、1 B、2 C、3 D、4
【分析】
哈夫曼树详细教程可以点这看:
哈夫曼树的画法,每次选取最小的两个结点组成二叉树。从剩下的结点和刚刚生成的结点中再选取两个最小的节点。最后生成一棵哈夫曼树。一般小的在左,大的在右。
从下图可以看出“也”字所处的位置是第三层,第L层的编码长度为L。所以长度是3。
16、关于汇编语言,下列说法错误的是( D )。
A、是一种与具体硬件相关的程序设计语言
B、在编写复杂程序时,相对于高级语言而言代码量较大,且不易调试
C、可以直接访问寄存器、内存单元、以及 I/O 端口
D、随着高级语言的诞生,如今已完全被淘汰,不再使用
【分析】汇编语言(Assembly Language)是任何一种用于电子计算机、微处理器、微控制器或其他可编程器件的低级语言,亦称为符号语言。面向机器的程序设计语言。在汇编语言中,用助记符代替机器指令的操作码,用地址符号或标号代替指令或操作数的地址。在不同的设备中,汇编语言对应着不同的机器语言指令集,通过汇编过程转换成机器指令。特定的汇编语言和特定的机器语言指令集是一一对应的,不同平台之间不可直接移植。D选项是不对的,汇编还有自己的用处。
17、(A )是一种选优搜索法,按选优条件向前搜索,以达到目标。当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择。
A、回溯法 B、枚举法 C、动态规划 D、贪心法
【分析】
A选项说的是回溯法,B选项枚举法是一个一个挨个尝试的方法,C选项动态规划是从全局考虑最终得出一个最优解,D选项贪心法,是从局部开始考虑出一个解,只是局部最优解,不一定是全局最优解。
18、1956 年( A )授予肖克利(William Shockley)、巴丁(John Bardeen)和布拉顿(Walter Brattain),以表彰他们对半导体的研究和晶体管效应的发现。
A、诺贝尔物理学奖
B、约翰·冯·诺依曼奖
C、图灵奖
D、高德纳奖(Donald E. Knuth Prize)
【分析】半导体的研究和晶体管,属于物理问题
19、对一个有向图而言,如果每个节点都存在到达其他任何节点的路径,那么就称它是强连通的。例如,右图就是一个强连通图。事实上,在删掉边( A )后,它依然是强连通的。
A、a B、b C、c D、d
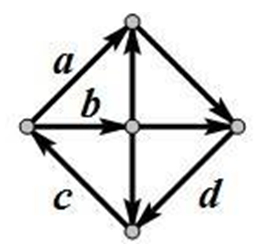
【分析】对于这个题,我们可以挨个试下,发现删除a,b,c,d,只有删除边a后,依然是强联通的。
20、从 ENIAC 到当前最先进的计算机,冯·诺依曼体系结构始终占有重要的地位。冯·诺依曼体系结构的核心内容是( C )。
A、采用开关电路 B、采用半导体器件
C、采用存储程序和程序控制原理 D、采用键盘输入
【分析】冯·诺依曼结构也称普林斯顿结构,是一种将程序指令存储器和数据存储器合并在一起的存储器结构。
二、问题求解(共 2 题,每题 5 分,共计 10 分)
1、每份考卷都有一个 8 位二进制序列号。当且仅当一个序列号含有偶数个 1 时,它才是有效的。例如,00000000、01010011 都是有效的序列号,而 11111110 不是。那么,有效的序列号共有___128___个。
【分析】
一共8位数,要求里面含偶数个1。那么前7位每位有2种不同的选法,前7位一共$2^7$种,当你确定了前面的7位之后,最后一位就自动确定了,因为前面7位如果是偶数个1,最后一位一定是0,前面7位如果是奇数个1,最后一位肯定是1。所以答案是$2^7=128$
2、定义字符串的基本操作为:删除一个字符、插入一个字符和将一个字符修改成另一个字符这三种操作。将字符串 A 变成字符串 B 的最少操作步数,称为字符串 A 到字符串 B 的编辑距离。字符串”ABCDEFG”到字符串”BADECG”的编辑距离为____3____。
【分析】
第一步:将A删除变成 BCDEFG
第二步:将C变成A变成 BADEFG
第三步:将F变成C变成 BADECG
注意,题目中只说了“删除”“插入”“修改”
三、阅读程序写结果(共 4 题,每题 8 分,共计 32 分)
1
#include <iostream>
using namespace std;
int main() {
int i, n, m, ans;
cin >> n >> m;
i = n;
ans = 0;
while(i <= m) {
ans += i;
i++;
}
cout << ans << endl;
return 0;
}
输入:10 20
输出:____165______
| i初值 | m初值 | while(i<=m) | ans | i |
| 10 | 20 | 10<=20 | 10 | 11 |
| 11<=20 | 21 | 12 | ||
| 12<=20 | 33 | 13 | ||
| 13<=20 | 46 | 14 | ||
| 14<=20 | 60 | 15 | ||
| 15<=20 | 75 | 16 | ||
| 16<=20 | 91 | 17 | ||
| 17<=20 | 108 | 18 | ||
| 18<=20 | 126 | 19 | ||
| 19<=20 | 145 | 20 | ||
| 20<=20 | 165 | 21 | ||
| 21<=20 (不成立) |
2
#include <iostream>
#include <string>
using namespace std;
int main() {
string map = "22233344455566677778889999";
string tel;
int i;
cin >> tel;
for(i = 0; i < tel.length(); i++)
if((tel[i] >= '0') && (tel[i] <= '9'))
cout << tel[i];
else if((tel[i] >= 'A') && (tel[i] <= 'Z'))
cout << map[tel[i] - 'A'];
cout << endl;
return 0;
}
输入:CCF-NOIP-2011
输出:__________________
【分析】
tel.length是测量字符串tel的长度。第一个if表示如果是0到9的数字字符,就直接输出,然后如果是大写字符,那么 map[ tel[i] – ‘A’ ] 表示的含义是 当前tel[i]的字符 减去 字符‘A’,比如当i=0时,tel[0] = C , ‘C’ -‘A’ = 2, 也就是map[2],然后查看map[2]结果是字符2。
| i | tel[i] | if | else if | tel[i]-‘A’ | map[tel[i]-‘A’] | 输出 |
| 0 | tel[0]=’C’ | 不成立 | 成立 | C-A=2 | map[2] | 2 |
| 1 | tel[1]=’C’ | 不成立 | 成立 | C-A=2 | map[2] | 2 |
| 2 | tel[1]=’F’ | 不成立 | 成立 | F-A=5 | map[5] | 3 |
| 3 | tel[3]=’-‘ | 不成立 | 不成立 | |||
| 4 | tel[4]=’N’ | 不成立 | 成立 | N-A=12 | map[12] | 6 |
| 5 | tel[5]=’O’ | 不成立 | 成立 | O-A=13 | map[13] | 6 |
| 6 | tel[6]=’I’ | 不成立 | 成立 | I-A=8 | map[8] | 4 |
| 7 | tel[7]=’P’ | 不成立 | 成立 | P-A=14 | map[7] | 7 |
| 8 | tel[8]=’-‘ | 不成立 | 不成立 | |||
| 9 | tel[9]=2 | 成立 | 不成立 | 2 | ||
| 10 | tel[10]=0 | 成立 | 不成立 | 0 | ||
| 11 | tel[11]=1 | 成立 | 不成立 | 1 | ||
| 12 | tel[12]=1 | 成立 | 不成立 | 1 |
3.
#include <iostream>
#include <cstring>
using namespace std;
const int SIZE = 100;
int main() {
int n, i, sum, x, a[SIZE];
cin >> n;
memset(a, 0, sizeof(a));
for(i = 1; i <= n; i++) {
cin >> x;
a[x]++;
}
i = 0;
sum = 0;
while(sum < (n / 2 + 1)) {
i++;
sum += a[i];
}
cout << i << endl;
return 0;
}
输入:
11
4 5 6 6 4 3 3 2 3 2 1
输出:_________3___
【分析】memset是初始化函数,第一个参数是函数名,第二个参数是初始化的值,第三个默认填sizeof(函数名)
第一个for循环,a[x]++ 是桶排,分别记录了下标出现的次数。
a[1]=1,a[2]=2,a[3]=3,a[4]=2,a[5]=1,a[6]=3
$\frac{n}{2}+1 =6 $
| while(sum<6) | i++ | sum+=a[i] |
| 0<6 | 1 | 1 |
| 1<6 | 2 | 3 |
| 3<6 | 3 | 6 |
| 6<6不成立 |
4.
#include <iostream>
using namespace std;
int solve(int n, int m) {
int i, sum;
if (m == 1)
return 1;
sum = 0;
for (i = 1; i < n; i++)
sum += solve(i, m - 1);
return sum;
}
int main() {
int n, m;
cin>>n>>m;
cout<<solve(n, m)<<endl;
return 0;
}
输入:7 4
输出:____20______
【分析】
| m=1 | m=2 | m=3 | m=4 | |
| n=1 | 1 | 0 | 0 | 0 |
| n=2 | 1 | 1 | 0 | 0 |
| n=3 | 1 | 2 | 1 | 0 |
| n=4 | 1 | 3 | 3 | 1 |
| n=5 | 1 | 4 | 6 | 4 |
| n=6 | 1 | 5 | 10 | 10 |
| n=7 | 1 | 6 | 15 | 20 |
四、完善程序(前 11 空,每空 2 分,后 2 空,每空 3 分,共计 28 分)
1、(子矩阵)输入一个n1*m1的矩阵a,和n2*m2的矩阵b,问a中是否存在子矩阵和b相等。若存在,输出所有子矩阵左上角的坐标;若不存在输出“There is no answer”
#include <iostream>
using namespace std;
const int SIZE = 50;
int n1, m1, n2, m2, a[SIZE][SIZE], b[SIZE][SIZE];
int main() {
int i, j, k1, k2;
bool good, haveAns;
cin >> n1 >> m1;
for(i = 1; i <= n1; i++)
for(j = 1; j <= m1; j++)
cin >> a[i][j]; //输入a数组
cin >> n2 >> m2;
for(i = 1; i <= n2; i++)
for(j = 1; j <= m2; j++)
____①____;
haveAns = false;
for(i = 1; i <= n1 - n2 + 1; i++)
for(j = 1; j <= ____②____; j++) {
____③____;
for(k1 = 1; k1 <= n2; k1++)
for(k2 = 1; k2 <= ____④____; k2++) {
if(a[i + k1 - 1][j + k2 - 1] != b[k1][k2])
good = false;
}
if(good) {
cout << i << ' ' << j << endl;
____⑤____;
}
}
if(!haveAns)
cout << "There is no answer" << endl;
return 0;
}
【分析】题目不是很难,可以靠猜做对大部分题目。
1.【 cin>>b[i][j] 】 上面双重for循环是读入a数组,下面这个双重for循环是读入b数组。
2. 【 m1-m2+1 】②所处的for循环是遍历整个二维数组的操作,根据上面i(行)所写的n1-n2+1,所以这个空填m1-m2+1
3. 【 good=true 】因为good没有初始化,下面又出现了将good变为false的操作,所以这个地方是将good初始化为true。
4. 【 m2 】④所处的双重for循环是检查子矩阵的过程,根据外层for循环的n2,这个空应该填m2。
5. 【havaAns = true】因为上方输出了i和j,所以说得到了答案,得到答案后将haveAns变为true。
2、(大整数开方)输入一个正整数n(1≤n<10100),试用二分法计算它的平方根的整数部分。
#include <iostream>
#include <string>
using namespace std;
const int SIZE = 200;
struct hugeint {
int len, num[SIZE];
};
//其中 len 表示大整数的位数;num[1]表示个位、num[2]表示十位,以此类推
hugeint times(hugeint a, hugeint b)
//计算大整数 a 和 b 的乘积
{
int i, j;
hugeint ans;
memset(ans.num, 0, sizeof(ans.num));
for(i = 1; i <= a.len; i++)
for(j = 1; j <= b.len; j++)
_____①_____ += a.num[i] * b.num[j];
for(i = 1; i <= a.len + b.len; i++) {
ans.num[i + 1] += ans.num[i] / 10;
_____②_____;
}
if(ans.num[a.len + b.len] > 0)
ans.len = a.len + b.len;
else
ans.len = a.len + b.len - 1;
return ans;
}
hugeint add(hugeint a, hugeint b)
//计算大整数 a 和 b 的和
{
int i;
hugeint ans;
memset(ans.num, 0, sizeof(ans.num));
if(a.len > b.len)
ans.len = a.len;
else
ans.len = b.len;
for(i = 1; i <= ans.len; i++) {
ans.num[i] += _____③_____;
ans.num[i + 1] += ans.num[i] / 10;
ans.num[i] %= 10;
}
if(ans.num[ans.len + 1] > 0)
ans.len++;
return ans;
}
hugeint average(hugeint a, hugeint b)
//计算大整数 a 和 b 的平均数的整数部分
{
int i;
hugeint ans;
ans = add(a, b);
for(i = ans.len; i >= 2; i--) {
ans.num[i - 1] += (_____④_____) * 10;
ans.num[i] /= 2;
}
ans.num[1] /= 2;
if(ans.num[ans.len] == 0)
ans.len--;
return ans;
}
hugeint plustwo(hugeint a)
//计算大整数 a 加 2 后的结果
{
int i;
hugeint ans;
ans = a;
ans.num[1] += 2;
i = 1;
while((i <= ans.len) && (ans.num[i] >= 10)) {
ans.num[i + 1] += ans.num[i] / 10;
ans.num[i] %= 10;
i++;
}
if(ans.num[ans.len + 1] > 0)
_____⑤_____;
return ans;
}
bool over(hugeint a, hugeint b)
//若大整数 a>b 则返回 true,否则返回 false
{
int i;
if(_____⑥_____)
return false;
if(a.len > b.len)
return true;
for(i = a.len; i >= 1; i--) {
if(a.num[i] < b.num[i])
return false;
if(a.num[i] > b.num[i])
return true;
}
return false;
}
int main() {
string s;
int i;
hugeint target, left, middle, right;
cin >> s;
memset(target.num, 0, sizeof(target.num));
target.len = s.length();
for(i = 1; i <= target.len; i++)
target.num[i] = s[target.len - i] - _____⑦_____
memset(left.num, 0, sizeof(left.num));
left.len = 1;
left.num[1] = 1;
right = target;
do {
middle = average(left, right);
if(over(_____⑧_____))
right = middle;
else
left = middle;
} while(!over(plustwo(left), right));
for(i = left.len; i >= 1; i--)
cout << left.num[i];
cout << endl;
return 0;
}
【分析】对结构体,高精度算法和二分法不太理解的有点难。
1.【ans.num[i+j-1] 】 这是在计算两个数的乘积,观察下面的代码部分,应该是ans.num,比较麻烦的是i+j-1
2. 【ans.num[i] % = 10】 这是进位操作,所以对10取余。
3. 【a.num[i] +b.num[i] 】 所处的add函数中,注释说计算a+b的和,所以应该填 a.num[i] +b.num[i]
4. 【 ans.num[i]%2 】 所处的函数是average 函数,根据注释 是计算平均数,看主过程,middle = average(left, right);就是求a和b的平均值,④所在循环是ans,已经等于a+b了,现在正在除以2,其实④处是退位。
5. 【ans.len++ 】 因为高位存在数字,所以将这个数字的长度加1
6. 【a.len < b.len 】over 函数,在主程序中这是一个二分用的判断函数,看到over中的if a.len > b.len这段,得知如果a比b长,也就是a比b大,那over 就为真,那么over函数就是比较大小的函数, a>b 为真,a<b 为假。 那么这个空跟下面的类似,应该是 a.len < b.len
7.【 ‘0’ 】 高精度计算中经常用到的字符转数字
8. 【 times(middle, middle),target 】比较难,通看全文,可以看出没有出现调用times函数的地方,所以这个地方应该是调用函数,这个地方应该是比较middle的平方与target
返回目录:NOIP/CSP信息学奥赛初赛