0.前言
上一篇我们主要介绍了二叉树的定义和相关规则,考试中有经常出现类似于“中缀表达式转后缀”,“前缀表达式转后缀”等。如果能画出唯一的二叉树那么便根据二叉树的结构之间求解即可,有些情况很难直接画出二叉树。还有通过加括号的方式进行求解,还有以下利用栈的这方法求表达式。
1.中缀转后缀
规则:
①从左往右遇到操作数直接输出
②遇到操作符,放入栈中
③遇到左括号,入栈
④遇到右括号,出栈(直到遇到左括号,左括号只弹出不输出)
⑤遇到其他操作符,弹出所有优先级大于或者等于该运算符的栈顶元素,然后将该运算符入栈
⑥最终将栈中元素依次输出
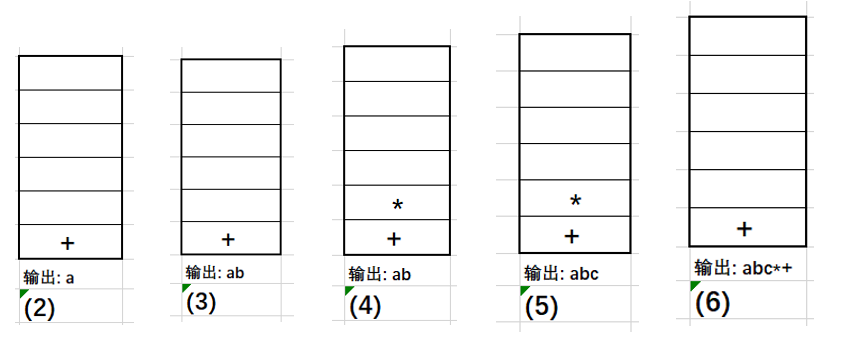
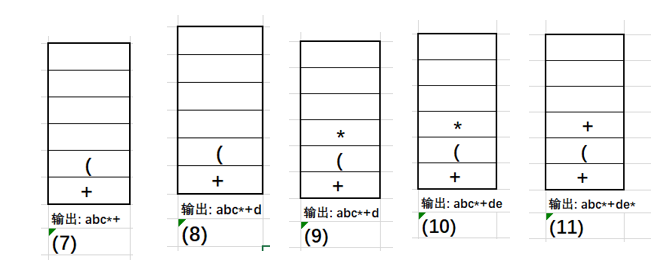
例如:a+b*c+(d*e+f)*g
方法:画图或画表
| 读入字符 | 栈内(底->顶) | 栈外 | 说明 |
| a | 空 | a | (1)操作数,直接输出 |
| + | + | a | (2)操作符,入栈 |
| b | + | ab | (3)操作数,直接输出 |
| * | +* | ab | (4)操作符,入栈(栈内没有优先级高于当前符合的) |
| c | +* | abc | (5)操作数,直接输出 |
| + | + | abc*+ | (6)上面第⑤步 |
| ( | +( | abc*+ | (7)左括号,入栈 |
| d | +( | abc*+d | (8)操作数,直接输出 |
| * | +(* | abc*+d | (9)操作符,入栈 |
| e | +(* | abc*+de | (10)操作数,直接输出 |
| + | +(+ | abc*+de* | (11)上面第⑤步 |
| f | +(+ | abc*+de*f | (12)操作数,直接输出 |
| ) | + | abc*+de*f+ | (13) 上面第④步 |
| * | +* | abc*+de*f+ | (14)操作符,入栈(栈内没有优先级高于当前符合的) |
| g | +* | abc*+de*f+g | (15)操作数,直接输出 |
| abc*+de*f+g*+ | (16) 上面第⑥步 |

2.中缀转后缀
规则:①从左往右,遇到数就入栈,遇到操作符就出栈
例如:24 8 + 3 * 4 10 7 – * /
方法1:画表

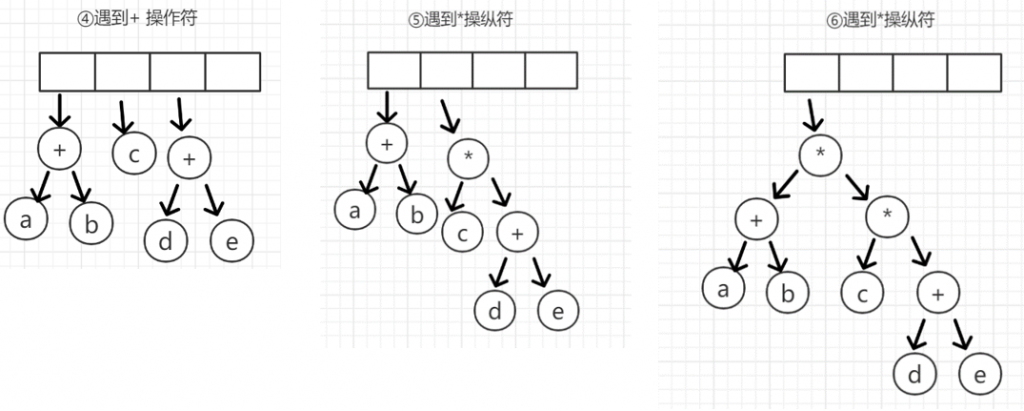
方法2:画二叉树 (例如: a b + c d e + * *)

3.前缀转中缀
跟后缀转中缀很类似
规则:从右往左,遇到数字就压栈,遇到操作符弹出栈顶两个元素,用运算符对他们相对它们做相应的计算,将结果入栈。重复上面过程。
例如:- × + 3 4 5 6
返回目录:NOIP/CSP信息学奥赛初赛