背包问题是一种资源分配算法,是一种非常典型的问题,是对资源分配最大化的体现。
倘若有n件物品,其中每件物品都有属于自己的质量和价值,现在仅有一个背包,但是背包最大的承载量为w,因此需要试图在这个背包里装一些物品,使得物品的价值之和最大且承载量不得超过背包的最大承载量。
背包问题根据选取物品的方式可以分为两种,一种是0-1背包问题,表示当前物品要么被选择要么不被选择;另外一种是部分背包问题,表示物品可以被拆分后选择商品的部分。整个物品的选择过程是独立事件,即在选择某件物品时与另外一件物品不存在关联关系。
0-1背包问题
0-1背包问题是指在某种情况下,可以采用穷举法的办法将所有物品的组合情况一一列出,然后选择在背包承重范围内价值最大的组合即可。这意味着,如果有n件物品,则组成的数量为2”种可能,因此每种物品都存在被选择或未被选择的可能。整个过程随着物品的增加呈现指数级增长,会有严重的性能问题。
除此之外,很容易想到的方法是,选择单位质量下价值最高的产品优先放入背包中,从直观而言似乎比较靠谱,但是通过实际分析却不尽如此。例如,存在一个承载量为10kg的背包,有若干商品,各物品质量和价值见下表。
| 物品 | 质量(Kg) | 价值(元) |
| A | 4 | 50 |
| B | 6 | 60 |
| C | 7 | 100 |
| D | 8 | 70 |
首先,分别计算每个物品在单位Kg下的平均价值,见下表:
| 物品 | 质量(Kg) | 价值(元) | 单位价值(元/Kg) |
| A | 4 | 50 | 12.5 |
| B | 6 | 60 | 10.0 |
| C | 7 | 100 | 14.3 |
| D | 8 | 70 | 8,75 |
其次根据上表中单位价值进行排序,依次为物品C、A、B、D,因此首先将C物品放入背包,但是由于背包限重10kg,因此当C物品放入背包之后,无法继续放其他物品到背包中,此时背包装载物品的价值为100元。
但是,选择物品A和物品B的组合可以获得最大价值110元,并且承重在背包的限制范围内,而仅放入C物品时则不仅达不到最大的价值还未能充分利用背包的承载量。如果物品的集合为a1,a2...,an,假设当取得ak物品之后,在满足背包承载范围的情况下达到背包内物品价值之和最大。那么,在放人ak物品之前的ax1物品则是满足在背包当前承重之下减去ax物品质量之下的最大价值之和,即在每次放入一个物品之前,它的最大价值应当是背包承载量减去还未放人的物品质量。因此,可以利用递推的关系进行推导,用w表示背包的承载量,w;表示第i个物品的本身质量,v;表示第i个物品的价值,c[i,w]表示到放入第i个物品为止,在限制承载量w下的物品价值之和的最大值,公式如下所示:
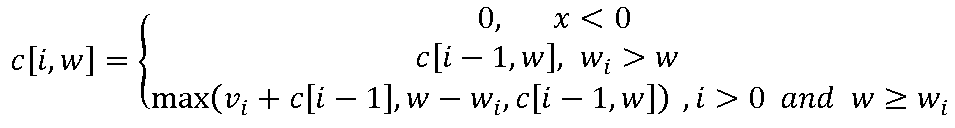
上述公式表示当在最初时刻或者背包不能承载量时,最大价值为0;当背包的剩余承载量不小于某个物品的质量时,纳入该物品;当没有商品能够填补背包剩余承载量时,当前即为价值之和的最大值。
部分背包
部分背包问题的解决方式与0-1背包不同,部分背包意味着物品可以拆卸。因此,可以按照前面介绍的单位质量下的价值,根据前面表格对单位价值进行排序后的结果见下表:
| 物品 | 质量(Kg) | 价值(元) | 单位价值(元/Kg) |
| C | 7 | 100 | 14.3 |
| A | 4 | 50 | 12.5 |
| B | 6 | 60 | 10.0 |
| D | 8 | 70 | 8.75 |
约定背包的限重依然为10kg,由于物品C的单位价值最大,因此首先放入物品C,然后放人A,但是由于物品A的质量为4kg,放入到背包之后背包超重,所以物品A并不能完全被放入,而最多只能放入3kg,因此物品A将被拆分,即仅能放入原始质量的3/4,价值也相应折扣为37.5元(12.5×3),最终背包累计得到的价值为137.5元(100+37.5)。
在实际的计算过程中,不会对单位质量的价值进行全部排序,因为超过背包质量的其他物品再进行排序也没有实质意义,例如,在表2-8中,物品C和A的质量之和已经超过了背包的限重,因此排序的物品C和A之后的B、D无须排序。
采用两种方式分析背包问题目的在于分析解决问题的本质。0-1背包问题是一个最优解的典型应用,不断从一个小的结果集中推导出全局最优的结果,采用的是动态规划思想的递归方法;而相对于部分背包问题,采用的是贪婪思想,每次选择当前最好的结果,然后不断得到一个最优的结果。