0.前言
查找是指在大量的数据中寻找特定的元素,它是数值计算中常用的运算逻辑。一般情况下,可以是按照顺序依次查找,但是在数据较大的情况下,顺序查找的性能往往会让人望而却步。折半查找和二分查找可以针对有序的数值序列做到快速查找,哈希查找则是针对无序的数值序列查找,它们都具有较好的性能。
1.二分搜索法
折半查找(Half—Interval—Search)也称作二分查找(Binary Search)、对数查找(Logarithmic Search),是指在有序的数值序列中,从中间开始进行查找,如果查找元素小于中间元素,则中间元素的左边区间再进行折半查找,如果查找元素大于中间元素,则在中间元素的右边区间再进行折半查找,直到取得的中间值等于查找的值或者查找的值不存在。
折半查找的最差时间复杂度为O(lg n),最优时间复杂度为O(1),平均时间复杂度O(lg n); 在采用递归的方式进行折半查找时,最差的空间复杂度为O(lg n),采用迭代的方式时,最差的空间复杂度为O(1)。总体而言,折半查找的查找性能较好,若对有序序列通过遍历的方式进行查找,则时间复杂度为O(n)。
同时,折半查找也可以按照二叉树的思想来理解,中间值等价于二叉树的根,根的左子树是中间值的前半部分,根的右子树是中间值的后半部分,并且折半查找再数据中的查找次数恰好等于二叉树的查找层次数。已有序列{1,3,4,6,9,10,12,13,16}为例子,构造一棵二叉树,使得对它的每个节点的左孩子都比当前节点的值小,右孩子都比当前节点的值大,如下图所示。
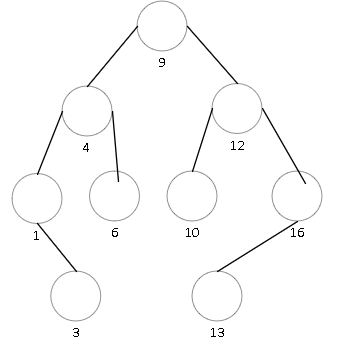
例如:当需要查找元素值11是否在此有序序列中时,可以根据上图按照如下方式进行查找:首先与二叉树的根节点9进行比较,11比9大,则向节点9的右子树进行比较,与右子树的根节点12进行比较,12比11大,于是向12的左子树根节点进行比较,10比11小,然而10已经是叶子节点,所以11不存在与该有序序列中。
利用二叉树的数据结构特征进行折半查找可以较好地理解查找过程,实质过程与利用数据的折半查找过程一致。良好的数据结构可以较好地理解查找过程,实质过程与利用数据的折半查找过程一致。良好的数据结构可以较好地解决数据与算法中的斜街问题。
与折半查找对应的是顺序查找(Sequential Search),顺序查找是一种最为直观的查找方式,通过从前往后的依次序列进行对比查找,由于查找的过程没有任何技巧,当被查找的原始不在序列中时,会把所有元素遍历一次。顺序查找的时间复杂度为O(n)。它的缺点是效率低下,时间复杂度高。折半查找避免了顺序查找中元素的一一比较问题,使得性能得到一定的提示,对于有序的查找应当尽量次啊用折半查找,对于无序序列可以采用顺序查找的方式。