【题目描述】
轩轩和凯凯正在玩一款叫《龙虎斗》的游戏,游戏的棋盘是一条线段,线段上有n个兵营(自左至右编号1∼n),相邻编号的兵营之间相隔 1 厘米,即棋盘为长度为n−1厘米的线段。i号兵营里有ci位工兵。
下面图1为n=6的示例:

轩轩在左侧,代表“龙”;凯凯在右侧,代表“虎”。他们以mm号兵营作为分界,靠左的工兵属于龙势力,靠右的工兵属于虎势力,而第mm号兵营中的工兵很纠结,他们不属于任何一方。
一个兵营的气势为:该兵营中的工兵数××该兵营到mm号兵营的距离;参与游戏一方的势力定义为:属于这一方所有兵营的气势之和。
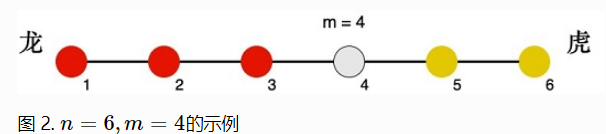
下面图2为n=6,m=4的示例,其中红色为龙方,黄色为虎方:
游戏过程中,某一刻天降神兵,共有s1位工兵突然出现在了p1号兵营。作为轩轩和凯凯的朋友,你知道如果龙虎双方气势差距太悬殊,轩轩和凯凯就不愿意继续玩下去了。为了让游戏继续,你需要选择一个兵营p2,并将你手里的s2位工兵全部派往兵营p2,使得双方气势差距尽可能小。
注意:你手中的工兵落在哪个兵营,就和该兵营中其他工兵有相同的势力归属(如果落在m号兵营,则不属于任何势力)。
【输入描述】
输入的第一行包含一个正整数n,代表兵营的数量。
接下来的一行包含nn个正整数,相邻两数之间以一个空格分隔,第i个正整数代表编号为i的兵营中起始时的工兵数量ci。
接下来的一行包含四个正整数,相邻两数间以一个空格分隔,分别代表m,p1,s1,s2。
【输出描述】
输出有一行,包含一个正整数,即p2,表示你选择的兵营编号。如果存在多个编号同时满足最优,取最小的编号。
【样例输入1】
6 2 3 2 3 2 3 4 6 5 2
【样例输出1】
2
【样例输入1说明】
见问题描述中的图 2。双方以m=4号兵营分界,有 s1=5 位工兵突然出现在 p1=6 号兵营。
龙方的气势为:
2×(4−1)+3×(4−2)+2×(4−3)=14
虎方的气势为:
2×(5−4)+(3+5)×(6−4)=18
当你将手中的 s2=2 位工兵派往 p2=2 号兵营时,龙方的气势变为:
14+2×(4−2)=18
此时双方气势相等。
【样例输入2】
6 1 1 1 1 1 16 5 4 1 1
【样例输出2】
1
【样例输入2说明】
双方以m=5号兵营分界,有 s1=1 位工兵突然出现在 p1=4 号兵营。龙方的气势为:
1×(5−1)+1×(5−2)+1×(5−3)+(1+1)×(5−4)=11 虎方的气势为:
16×(6−5)=16
当你将手中的 s2=1位工兵派往 p2=1 号兵营时,龙方的气势变为:
11+1×(5−1)=15
此时可以使双方气势的差距最小。
【数据规模】
1<m<n, 1≤p1≤n
对于 20% 的数据,n=3,m=2,$c_i$=1,$s_1,s_2$≤100。
另有 20% 的数据,n≤100,$p_1$=m,$c_i=1,s_1,s_2$≤100
对于 60% 的数据,n≤100,$c_i=1,s_1,s_2$≤100
对于 80% 的数据,n≤100,$c_i,s_1,s_2$≤100
对于 100% 的数据,n≤$10^5,c_i,s_1,s_2≤10^9$。
【分析】
1.题目要求在p2位置放s2达到 尽可能平衡的状态。“尽可能的小”。
2.建议开 long long ,否则遇到大的样例过不去。
3.m是中立的,不属于任何一方。
4.多个编号同时满足,输出最小的那个。
5.“天降神兵”,有没有可能落在m处(中立处)。
6. 左边是龙 ,右边是虎。
7.当龙的气势大于虎的气势的时候,不一定要把s2放到气势弱的一方,因为有可能你引入s2后,比原来的气势差还大。
【思路1】
先计算出双方的气势,再加上s1的值。求双方的气势差,从“弱”的一方开始扫描,求每次的气势差,取最小的那次即可。
【参考代码1】
#include<cstdio>
#include<iostream>
using namespace std;
long long c[100010]; //
long long m,p1,s1,s2,p2; //定义中立点m,天降神兵的位置p1,天降神兵的数量s1,你手里的工兵的数量s2, 你要放s2的位置
long long qishil[100010],qishih[100010],suml,sumh; // 定义龙每个点的气势,虎每个点的气势,龙总气势,虎总气势
long long minn =1e9; //定义极小值
int main() {
int n;
scanf("%d",&n);
for(int i=1; i<=n; i++)
scanf("%lld",&c[i]); //读入每个点工兵数
scanf("%lld%lld%lld%lld",&m,&p1,&s1,&s2); //读入数据
//开始龙每个点的气势和总气势
for(int i=1; i<m; i++) {
qishil[i]=(m-i)*c[i];
suml+=qishil[i];
}
//开始计算虎每个点的气势和总气势
for(int i=n; i>m; i--) {
qishih[i]=(i-m)*c[i];
sumh+=qishih[i];
}
//计算天降神兵后的气势
if(p1<m)
suml+=s1*(m-p1);
if(p1>m)
sumh+=s1*(p1-m);
p2=m; //先让p2 在m处,
//计算p2的位置
if(suml==sumh) { //龙虎气势相等,s2肯定放到m处
p2=m;
} else if(suml>sumh) { //龙的气势大于虎的,
long long temp,dis; //分别表示每次的最小值和原来的气势差
dis=suml-sumh;
for(long long i=m+1; i<=n; i++)
{
temp=sumh + (i-m)*s2 -suml; //计算每次的差值
temp= temp>0?temp:-temp;
if(temp<minn && temp<dis) // 不仅要小于最小值,还要小于原来的气势差 ,不这样的话就保留p2在m处
{
minn=temp;
p2=i;
}
}
} else { //否则就是虎的气势大于龙的气势,
long long temp,dis;
dis = sumh-suml;
for(long long i=1; i<m; i++)
{
temp =suml+ (m-i)*s2 -sumh; //计算每次的差值
temp =temp>0?temp:-temp;
if(temp<minn && temp<dis) // 不仅要小于最小值,还要小于原来的气势差
{
minn=temp;
p2=i;
}
}
}
printf("%lld",p2);
return 0;
}返回目录:NOIP/CSP信息学奥赛复赛