【题目描述】
传说很遥远的藏宝楼顶层藏着诱人的宝藏。小明历尽千辛万苦终于找到传说中的这个藏宝楼,藏宝楼的门口竖着一个木板,上面写有几个大字:寻宝说明书。说明书的内容如下:
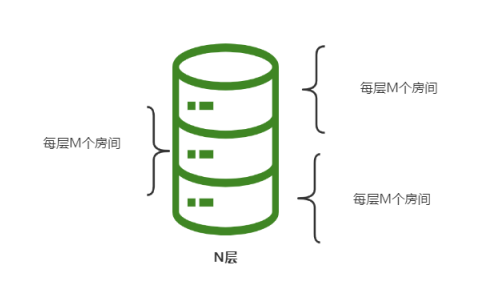
藏宝楼共有 N+1 层,最上面一层是顶层,顶层有一个房间里面藏着宝藏。除了顶层外,藏宝楼另有 N 层,每层 M 个房间,这 M 个房间围成一圈并按逆时针方向依次编号为 0,…,M-1。其中一些房间有通往上一层的楼梯,每层楼的楼梯设计可能不同。每个房间里有一个指示牌,指示牌上有一个数字 x,表示从这个房间开始按逆时针方向选择第 x 个有楼梯的房间(假定该房间的编号为 k),从该房间上楼,上楼后到达上一层的 k 号房间。比如当前房间的指示牌上写着 2,则按逆时针方向开始尝试,找到第 2 个有楼梯的房间,从该房间上楼。
如果当前房间本身就有楼梯通向上层,该房间作为第一个有楼梯的房间。寻宝说明书的最后用红色大号字体写着:“寻宝须知:帮助你找到每层上楼房间的指示牌上的数字(即每层第一个进入的房间内指示牌上的数字)总和为打开宝箱的密钥”。
请帮助小明算出这个打开宝箱的密钥。
【输入描述】
第一行 2 个整数 N 和 M,之间用一个空格隔开。N 表示除了顶层外藏宝楼共 N 层楼,M 表示除顶层外每层楼有 M 个房间。
接下来 N*M 行,每行两个整数,之间用一个空格隔开,每行描述一个房间内的情况,其中第(i-1)*M+j 行表示第 i 层 j-1 号房间的情况(i=1, 2, …, N;j=1, 2, … ,M)。第一个整数表示该房间是否有楼梯通往上一层(0 表示没有,1 表示有),第二个整数表示指示牌上的数字。注意,从 j 号房间的楼梯爬到上一层到达的房间一定也是 j 号房间。
最后一行,一个整数,表示小明从藏宝楼底层的几号房间进入开始寻宝(注:房间编号从 0 开始)。
【输出描述】
输出只有一行,一个整数,表示打开宝箱的密钥,这个数可能会很大,请输出对 20123取模的结果即可。
【样例输入1】
2 3 1 2 0 3 1 4 0 1 1 5 1 2 1
【样例输出1】
5
【样例说明】
第一层:
0 号房间,有楼梯通往上层,指示牌上的数字是 2;
1 号房间,无楼梯通往上层,指示牌上的数字是 3;
2 号房间,有楼梯通往上层,指示牌上的数字是 4;
第二层:
0 号房间,无楼梯通往上层,指示牌上的数字是 1;
1 号房间,有楼梯通往上层,指示牌上的数字是 5;
2 号房间,有楼梯通往上层,指示牌上的数字是 2;
小明首先进入第一层(底层)的 1 号房间,记下指示牌上的数字为 3,然后从这个房间开始,沿逆时针方向选择第 3 个有楼梯的房间 2 号房间进入,上楼后到达第二层的 2 号房间,记下指示牌上的数字为 2,由于当前房间本身有楼梯通向上层,该房间作为第一个有楼梯的房间。因此,此时沿逆时针方向选择第 2 个有楼梯的房间即为 1 号房间,进入后上楼梯到达顶层。这时把上述记下的指示牌上的数字加起来,即 3+2=5,所以打开宝箱的密钥就是 5。
【数据说明】
对于 50%数据,有 0<N≤1000,0<x≤10000;
对于 100%数据,有 0<N≤10000,0<M≤100,0<x≤1,000,000。
【分析】
- 题目比较长,但是读明白后发现是一道模拟题,细节比较坑。
- 房间编号从0开始。从j号房间上去,一定也是j号房间。
- 房间是一个环,看到题目中x的范围一定要想规律(房间一共就那么多,假如就4个房间,x=99999的话,难道真的挨个查到99999吗,所以要考虑周期性问题)
- 每次运算中取模就不用开long long了
- 如果一开始所在房间有楼梯,记得也要算进去
- 要记录下每一层有房间的个数
- 即每层第一个进入的房间内指示牌上的数字的总和为密码
- 不建议使用三维数组,可以转换为二维数组
【关于优化的部分】
假如某一层只有3个有楼梯的房间,当x=1000时,需要模拟1000次。然而1000%3=1,模拟1次就够了
【参考代码】
#include<iostream>
#include<cstdio>
using namespace std;
const int N(10008),M(108),MODN=20123;
int a[N][M],f[N][M],sum[N]={0};
int main()
{
//freopen("treasure.in","r",stdin);
//freopen("treasure.out","w",stdout);
int n,m,i,j,k;
scanf("%d%d",&n,&m);
for (i=1;i<=n;i++)
for (j=0;j<m;j++)
{
scanf("%d%d",&f[i][j],&a[i][j]);
if (f[i][j]) sum[i]++;
}
int ans=0;
scanf("%d",&j);
for (i=1;i<=n;i++)
{
ans=(ans+a[i][j])%MODN;
a[i][j]%=sum[i];
if (a[i][j]==0) a[i][j]=sum[i];
for (k=a[i][j];k>0;)
{
if (f[i][j])
k--;
if (k>0) j=(j+1)%m;
}
}
printf("%d\n",ans);
return 0;
}
返回目录:NOIP/CSP信息学奥赛复赛