信息学奥赛知识点(五)—进制转换

一、进位计数制的基本概念

将数字符号按排列成数位，并遵照某种由低到高的进位方式计数表述数值的方法，称为计数制。

1.十进制

十进制计数由0,1,2,3,4,5,6,7,8,9共10个数字符号组成。相同数字符号在不同的数位上表示不同的数值，每个数位计满十就向高位进一 ，即“逢十进一”

2.八进制

“逢八进一”

3.二进制

“逢二进一”

4.十六进制

1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

5.基数和权

	K2	K1	K0	小数点	K-1	K-2
J=2	22=4	21=2	20=1		2-1=0.5	2-2=0.25
J=8	82=64	81=8	80=1		8-1=0.125	8-2=0.015625
J=10	102=100	101=10	100=1		10-1=0.1	10-2=0.01
J=16	162=256	161=16	160=1		16-1=0.0625	16-2=0.00390625

二、数制之间的转换

计算机内部使用的数字符号只有0和1两个。也就是说，计算机内部使用的是二进制数，所有数值数据和非数值数据，都是有0和1这两个数字符号加以组合而成的，我们称之为“二进制代码”。

为了方便期间，常在数字后面加一个缩写字母后缀作为不同进制的数标识，各种进制数的后缀字母：

       B:二进制        O：八进制

       D:十进制     H：十六进制

    对于十进制，通常不加后缀，

1.二进制与十进制的转换

(1)二进制转十进制

方法1：按权展开法 例如 ：  (1011.01)₂

权	K3	K2	K1	K0	小数点	K-1	K-2
权值	8	4	2	1		0.5	0.25
系数	1	0	1	1		0	1
对于值	8	0	2	1		0	0.25

结果8+0+2+1+0+0.25=11.25

（2）十进制转二进制

方法1：按权展开法

类似于拼凑出合适的数字，例如（89）₁₀

          对于89这个数字来说，考虑2的次方关系，寻找和89最近的这个数,  2⁶=64 <89 <2⁷=128,所以在2⁶ 的系数为1。剩余89-64=25。则继续考虑25。  2⁴=16 <25 <2⁵=32。所以2⁴

处系数为1。剩余25-16=9。2³=8，2⁰=1

权	K7	K6	K5	K4	K3	K2	K1	K0
权值	128	64	32	16	8	4	2	1
系数		1		1	1			1

则结果为（1011001）₂

方法2：

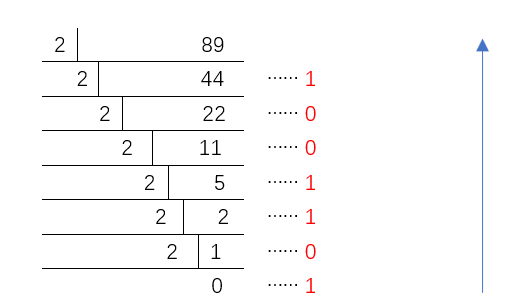
十进制整数转二进制数： “除2取余，逆序输出”

例如：（89）₁₀ =（1011001）₂

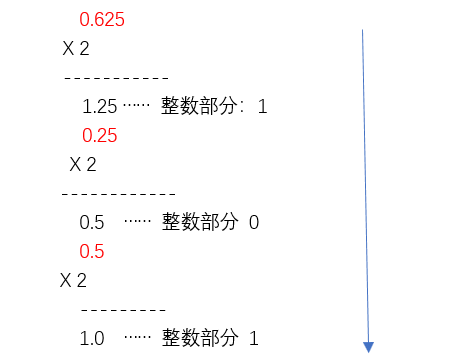
十进制小数转二进制数： “乘2取整，顺序输出”

例如：（0.625）₁₀ =（0.101）₂

---

2.八进制与二进制的转换

(1)八进制转二进制

每一个八进制的数都表示成一个三位二进制
方法：把每一位按权展开法

例如：（37.416）₈=（11111.10000111）₂

八进制	3	7	.	4	1	6
二进制	011	111		100	001	110

把高位和低位的0去掉后就是（11111.10000111）₂

（2）二进制转八进制

例如：（10110.0011）₂

方法：每三位二进制组成一位八进制

二进制	010	110	.	001	100
八进制	2	6		1	4

三位为一组，不足三位的补0

---

3.十六进制与二进制的转换

(1)十六进制进制转二进制

例如：（5DF.9）₁₆=（10111011111.1001）₂

十六进制	5	D	F	.	9
二进制	0101	1101	1111	.	1001

把高位和低位的0去掉后就是（10111011111.1001）₂

(2)二进制进制转十六进制

 方法：从小数点开始往左往右每四位组成一个十六进制

 例如：（1100001.111）₂

二进制	0110	0001	.	1110
十六进制	6	1		E

---

4.八进制与十进制的转换

把这个八进制的最后一位乘上8⁰,倒数第二位8¹，一直乘到最高位，然后把各项乘积相加，结果即为十进制。

（36）₈= 3*8¹ + 6*8⁰ =24+6 =(30)₁₀

---

5.十六进制与十进制的转换

把这个十六进制的最后一位乘上16⁰,倒数第二位16¹，一直乘到最高位，然后把各项乘积相加，结果即为十进制。

（1E）₁₆= 1*16¹ + 14*16⁰ =16+14 =(30)₁₀

---

返回目录：NOIP/CSP信息学奥赛初赛

---