朴素贝叶斯分类器的特征条件独立假设并基于贝叶斯定理的分数方法,它是一种非常传统的分类方法,有着较深的基础数学理论基础。相对而言,朴素贝叶斯分类器的分类效果比较稳定,在分类过程中对样本的每个特征都做了不相关假设
1.有监督分类与无监督分类
机器学习算法分为有监督学习和无监督学习。根据分类识别前是否需要进行训练,可将分类再划分为由监督分类(Supervised Classification)和无监督分类(Unsuperivised Calssification)
有监督分类是指根据已有的训练集提供的样本,通过不断计算,从样本中学习选择特征参数,对分类器建立判别函数以对被识别的样本进行分类。首先它需要一定量级的训练数据,通过对训练数据进行特征提取,最终形成符合特征的分类模型,最终分类模型形成分类器,实现对数据的分类。有监督分类方式可以有效利用先验数据,对后验数据进行校验,但是缺点也比较明显。首先,训练数据是人为收集,具有一定的主观性,并且人为收集数据也会导致花费一定的人力成本;其次,最终分类器分类的结果中,分类结果只可能是训练数据中的分类类型,不会产生新的类型。
无监督分类是指对分类器不事先进行先验知识学习,不时模型进行参数训练,使用被分类的样本数据直接进行分类的过程。此类分类过程只是对不同类别的数据进行分类区分,对分类后的类别特征不能确定。采用无监督的分类方式,对分类结果的选择性较大,不局限于某一特定的分类类型,且该过程由于是无监督过程,所以人为干预较少,结果具备一定的客观性。但是无监督分类的方式一般计算过程较为复杂,需要进行大量的分析后才可能获得较好的分类结果。
无监督分类和有监督分类的实质分别是指在机器学习中有监督学习和无监督学习的实例,它们的特征是有监督学习和无监督学习的一部分。除此之外,还有半监督学习(Semi-supervised Learning),它是在建立已有模型的基础上,再通过从少量训练样本中获得先验数据的机器学习方式,结合了有监督学习和无监督学习的各自优势。
在机器学习领域,有两个对结果影响非常大的因素,一个是语料库,另一个是算法模型。在非监督学习中,算法模型起核心作用;在监督学习中,语料库和算法模型相辅相成,有时一个合适的语料库对系统的改进效果甚至超过了对一个算法模型的改进。
2.一个例子
(1)我们采集了樱桃和车厘子的相关特征数据,然后考虑下面的问题:
通过现有的的车厘子和樱桃的数据,在包含车厘子和樱桃的混合水果中,随机给一个车厘子或者樱桃,识别它是樱桃或者车厘子的可能性哪个大?
| 水果类型 | 鲜红值(色度比) | 直径(cm) | 质量(g) |
| 车厘子 | 0.81 | 1.02 | 8.85 |
| 车厘子 | 0.82 | 0.98 | 8.67 |
| 车厘子 | 0.78 | 0.99 | 8.75 |
| 车厘子 | 0.79 | 1.01 | 8.80 |
| 樱桃 | 0.56 | 0.85 | 7.32 |
| 樱桃 | 0.58 | 0.86 | 7.33 |
| 樱桃 | 0.59 | 0.83 | 7.29 |
| 樱桃 | 0.57 | 0.84 | 7.31 |
(2)贝叶斯定理
在利用朴素贝叶斯(Naive Beyesian)解决问题之前,首先需要了解贝叶斯定理(Bayes'Theorem),因为朴素贝叶斯是以贝叶斯定理为基础的概率分类模型。贝叶斯定理是概率论中的一个定理,它跟随机变量的条件概率及边缘概率分布有关。在有些关于概率的解说中,贝叶斯定理能够告知我们如何利用新证据修改已有的看法。这个名称来自于托马斯·贝叶斯。
通常,事件A在事件B(发生)的条件下的概率与事件B在事件A的条件下的概率是不一样的;然而,这两者有着确定的关系,贝叶斯定理就是对这种关系的表示。贝叶斯公式定义在事件B出现的前提下,事件A出现的概率等于事件A出现的前提下事件B发生的概率乘以时间A出现的概率再除以时间B出现的概率。通过联系事件A与事件B,计算从一个事件产生另一事件的概率,即从结果上溯原。因此,贝叶斯定理公式如下所示:
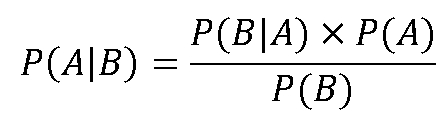
在理解贝叶斯定理的基础上,可以较好地理解基于朴素贝叶斯的分类模型。信息分类是信息处理中最基本的模块,每一段信息无论长或短,都由若干特征组成,因此可以将所有特征视为一个向量集W=(w1,w2,W3,···,wn),其中w;即表示其中第i个特征。而信息的分类也可以视为一个分类标记的集合C={c1,C2,C3,···,cm}。在进行特征学习之前,特征 wi与分类标记cj的关系不是确定值,因此需要提前计算P(CIW),也就是在特征w出现的情况下,信息属于分类标记C的概率,可根据贝叶斯计算,公式如下:
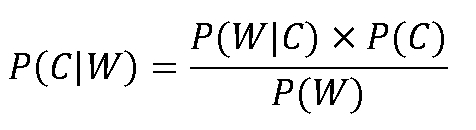
因此,可以从信息分类的角度理解贝叶斯公式,即表示为:在特征w,出现的情况下是否是特征类别c;取决于在特征分类标记cy情况下特征w,出现的概率以及w;在所有特征中出现的概率。P(W)的意义在于如果这个特征在所有信息中出现,那么用特征w,去判定是否属于分类标识cj的概率越低,越不具备代表性。
(3)问题解决
朴素贝叶斯是一种有监督的学习方式,可以利用伯努利模型(Bernoulli Model)以文件为粒度进行文本分类,假设训练样本集的特征满足高斯分布,如下表
| 类型 | 均值(鲜红比) | 标准差(鲜红比) | 均值(直径) | 标准差(直径) | 均值(质量) | 标准差(质量) |
| 车厘子 | 0.8 | 0.018257419 | 1 | 0.018257419 | 8.7675 | 0.076757193 |
| 樱桃 | 0.575 | 0.012909944 | 0.845 | 0.012909944 | 7.3125 | 0.017078251 |
我们认为两种类别的等概率的,也就是p(车厘子)=p(樱桃)=0.5。概率密度函数如下:
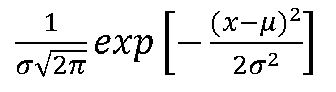
验证过程先给出一个待确定属于车厘子还是樱桃的测试样本,如下:
| 类别 | 鲜红值 | 直径(cm) | 质量(g) |
| Unknow | 0.8 | 0.86 | 8 |
验证的标准是:得到的样本属于樱桃还是车厘子的后验概率大者。

上述式子用于求取车厘子的后验概率

上式用于求取樱桃的后验概率。证据因子evidence(通常是常数)用来对各类的后验概率之和进行归一化处理。
evidence=p(车厘子) * p(鲜红值|车厘子) * p(直径|车厘子) * p(质量|车厘子)+
p(樱桃) * p(鲜红值|樱桃) * p(直径|樱桃) * p(质量|樱桃)
证据因子是一个常数(在高斯分布中通常是一个常数),所以可以忽略,只需计算后验概率式子中的分子即可。接下来通过样本的特征值来判别样本所属的类别。
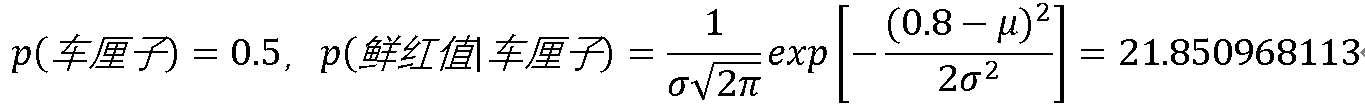
其中,

二者均为训练集样本的高斯分布参数。注意,这里计算的是概率密度而不是概率。

通过上述计算可以看出,车厘子的后验概率较大,由此可以预计这个样本属于车厘子的可能性较大。
3.分类流程归纳
贝叶斯分类是一系列分类算法的总称,这类算法均以贝叶斯定理为基础。贝叶斯算法是200多年前发明的算法,在信息领域中广泛运用,有着无法取代的地位。朴素贝叶斯算法是贝叶斯分类中运用最为广泛的分类算法之一。朴素贝叶斯算法起源于古典数学理论,有着坚实的数学基础及稳定的分类效率。朴素贝叶斯分类器模型所需的参数很少,算法也比较简单,便于理解学习。在属性个数较少或属性之间关联性较小时,利用朴素贝叶斯算法对数据进行分类往往能达到较好的效果,且误差率比使用另一分类模型–决策树模型时更小。
针对不同的问题算法得出的结果不同。因为算法对属性的识别情况取决于很多因素,所以不能断定在某种情况下哪个分类模型更优,这需要根据实际问题来进行选择。
经过上述流程分析,可以将朴素贝叶斯进行分类的流程大致定义为数据准备阶段、分类器训练阶段及分类识别阶段。
(1)数据准备。数据准备是语料库的准备工作阶段,这个阶段的任务是为朴素贝叶斯分类做必要的准备,主要工作是根据具体情况确定特征属性,并对每个特征属性进行适当划分,然后人工对一部分待分类项进行分类,形成训练样本集合。这一阶段输人的是所有待分类数据,输出的是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段,其质量对整个过程将有重要影响,分类器的质量很大程度上基于特征属性、特征属性划分及训练样本质量决定。
(2)分类器训练。这个阶段的任务就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率,以及每个特征属性划分对每个类别的条件概率估计,并记录结果。其输入是特征属性和训练样本,输出是分类器。这一阶段是机械性阶段,根据前面讨论的公式可以由程序自动计算完成。
(3)分类识别。这个阶段的任务是使用分类器对待分类项进行分类,其输人是分类器和待分类项,输出是待分类项与类别的映射关系。这一阶段也是机械性阶段,由程序完成。
分类的方式方法林林总总,此种方法以文档为粒度进行分析,也可以采用词频的方式进行分析,还可以采用TF-IDF然后加权求值的方式。
在分类结果中,常常需要将数值归一化,尤其是对分类器训练的结果。归一化的目的是让每个词在不同分类上的权重对应到区间(0,1),以使语料库中的词在相同分类的权值相加变得更有可比性。
4.常用评价指标
一切算法都有其评价的标准,时间复杂度和空间复杂度是算法关于性能的评价标准。除此之外,还需要对算法进行效果的评估,这种效果体现的是功能上的效果,如结果是否符合预期、能够满足需求等。在机器学习算法领域最为广泛且为大众熟知的评价指标是正确率(Accuracy)、精确度(Precision)及召回率(Recall)。基于正确率、精确度和召回率的模型更容易被大众理解和接受,也是最容易执行验证的标准。
在了解正确率、精确度、召回率之前,假设某个分类器的目标有且仅有两类,分别是正例(Positive)和负例(Negtive),现在首先了解一些常用的术语。
(1)TP(True Positives):被分类为正例的个数,即被分类器划分为正例且本身也是正例的个数。
(2)FP(False Positives):被错误地分类为正例的个数,即被分类器划分为正例但是实际上是负例的个数。
(3)FN(False Negatives):被错误地分类为负例的个数,即被分类器划分为负例但是实际上是正例的个数。
(4) TN (True Negatives):被正确地分类为负例的个数,即被分类器划分为负例且实际上也是负例的个数。
根据上述表述,所有的正例样本数P=TP+FN,负例样本数N=FP+TN,各个评价指标如下所示。
(1)正确率。
Accuracy=(TP+TN)÷(P+N),即被准确识别为正例和负例的个数除以总的样本数量,可以理解为达到期望的结果数量与总数的比。
(2)精准度。
Precision=TP÷(TP+FP),即所有识别为正例的个数中真正属于正例的数量比,可以理解为正例的识别正确率。
(3)召回率。
召回率是对算法覆盖面的度量,recall=TP÷(TP+FN)即所有正例样本中,被识别为正例的比率。
(4)错误率。
错误率与正确率相反,表现的是算法的错误程度。
从上述过程可知,召回率与正确率并无直接关系,但是从实际工程角度,尤其是在大规模数据量中,二者却又是相互制约的。在分类别是过程中,若分类器希望区分出更多正例实例,则这时也会有很多负例文档被搜索出来,从而使正确率受到影响;同理,试图减少负例实例时,也会使部分正例的实例被排除在外,从而影响召回率。二者的关系是召回率高时,正确率低;召回率低,趋势如下图:

在实际的评价过程中,区分算法的优劣势不在于准确率或召回率单一因素。很难做到均处于高位,因此需要在二者之间寻找平衡,这个平衡后的综合因素,采用F度量。
F度量的公式为:

一般情况下取λ=0.5,因此可以将公式简化为
F=正确率*召回率*2/(正确率+召回率)
F 值可认为是精准度和召回率的调和平均值。调和平均与通常的几何平均、算术平均不同。调和平均值强调较小数值的重要性,对小数值比较敏感,用于机器学习算法的正确率和召回率比较合适,因为系统试图尽可能让精准度和召回率都比较高。 通过F值的计算可以使精准度和召回率之间得到一定平衡。在所有的机器学习算法中,不能仅简单计算一个样本的F值,还需要计算更多样本的F值,并需要对n组进行测,然后求平均,公式如下所示:
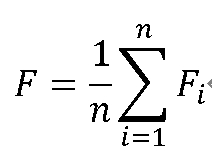
正确率是一个非常直观的评价指标,但是正确率并不一定能够代表一个算法的优劣,尤其在低概率事件中。例如,利用一种预测算法去预测某地区是否发生海啸,一般而言,发生海啸的概率是极低的,预测的结果只有:发生海啸、不发生海啸。如果一个预测算法把所有样本数据不假思索地划分为不发生海啸,则预测算法的准确率可以达到90%以上,但是当这个地区真正发生海啸时,这个预测算法一点效果也没有,形同虚设。在数据不均匀分布的情况下,一味地追求准确率则会忽视算法本身的价值。
在机器学习算法中,除上述评价指标外,还有很多其他的评价指标,如下所示。
(1)错误率。错误率(Error Rate)和上述的正确率相对,描述在信息处理过程中错误的比率。
(2)鲁棒性。鲁棒性是针对在数据处理过程中,可以训练过程中缺失数据和异常数据的处理能力。一般情况下,鲁棒性越高,说明该算法越智能。
(3)计算复杂度。计算复杂度依赖于具体的实现细节和硬件环境。在数据挖掘中,由于操作对象是巨量的数据库,所以空间和时间的复杂度问题将是非常重要的一个环节。
(4)模型描述的简洁度。对于描述型的分类任务,模型描述越简洁越受欢迎。例如,采用规则表示的分类器构造法就更有用。
之所以会有这么多的指标对机器学习算法进行评价,是由于机器学习的算法在社会发展的方方面面都会被使用到,从而导致在不同场景使用得到的期望不尽相同,需要采用不同的评价指标,引导结果向最初期望的方向发展。例如,错误率和正确率本身表达的含义虽然不相同,但是实质表现的含义却一致,当对一些高精度进行分析时(如航天工业),则追求错误率极低,初粒度的分析(天气预报)则追求高正确率。
在对测试样本进行正确率进行测试时,有可能因为过分拟合而导致测试的结果相对较好,所以更好的测试方法是,在训练集进行构造时,将训练数据分为两部分,一部分用于训练构造器,另一部分用于机器学习的各项评估。