0.前言
搜索与回溯是计算机解题中常用的算法,很多问题无法根据某种确定的计算法则来求解,可以利用搜索与回溯的技术求解。回溯是搜索算法中的一种控制策略。它的基本思想是:为了求得问题的解,先选择某一种可能情况向前探索,在探索过程中,一旦发现原来的选择是错误的,就退回一步重新选择,继续向前探索,如此反复进行,直至得到解或证明无解。
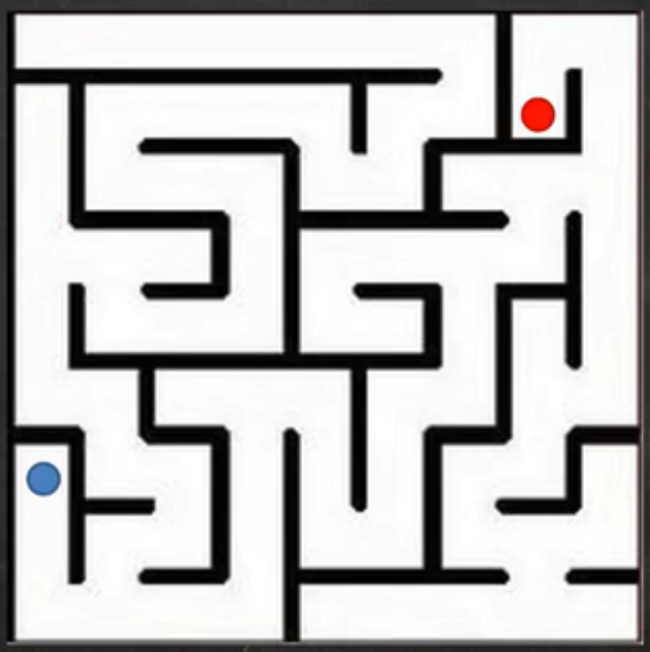
如迷宫问题:进入迷宫后,先随意选择一个前进方向,一步步向前试探前进,如果碰到死胡同,说明前进方向已无路可走,这时,首先看其它方向是否还有路可走,如果有路可走,则沿该方向再向前试探;如果已无路可走,则返回一步,再看其它方向是否还有路可走;如果有路可走,则沿该方向再向前试探。按此原则不断搜索回溯再搜索,直到找到新的出路或从原路返回入口处无解为止。
1.基本概念
(1)什么是搜索?
搜索是计算机程序设计中一种最基本、最常用的算法。搜索算法是直接基于计算机高速运算的特点而使用的计算机求解方法。它是从问题的初始状态出发,根据其中的约束条件,按照一定的策略,有序推进,不断深入,对于达到的所有目标状态(解空间),一一验证,找到符合条件的解(可行解),或者找出所有可行解中的最优解。
(2)什么是回溯
“回溯法”也称“试探法”。它是从问题的某一状态出发,不断“试探”着往前走一步,当一条路走到“尽头”,不能再前进(拓展出新状态)的时候,再倒回一步或者若干步,从另一种可能的状态出发,继续搜索,直到所有的“路径(状态)”都一一试探过。这种不断前进、不断回溯,寻找解的方法,称为“回溯法”。深度优先搜索求解的时候,当找到目标结点之后,还要回头寻找初始结点到目标结点的解路径。而回溯法则不同,找到目标结点之后,搜索路径就是一条从初始结点到目标结点的解路径。回溯法实际上是状态空间搜索中,深度优先搜索的一种改进,是更实用的一种搜索求解方法。
(3)搜索跟回溯的关系
- 深度优先搜索包含回溯,或者说回溯法是深度优先搜索的一种。
- 深度优先搜索需要控制如何实现状态之间的转移(拓展),回溯法就是深度优先搜索的一种控制策略。
- 回溯的过程中,并不需要记录整棵“搜索树”,而只需记录从初始状态到当前状态的一条搜索路径,是“线性链状”的,其最大优点是占用空间少。
- 深度优先搜索可以采用递归(系统栈)和非递归(手工栈)两种方法实现。递归搜索是系统栈实现一部分的回溯(如果需要记录一些特殊信息或较多的信息,还需要另外手工记录),而非递归是自己用手工栈模拟回溯的过程,所以实现起来略为复杂一点。
(4)案例分析
如何理解回溯:
某一天,一位牧师在森林里散步,他一不小心脚滑了,嗯,是脚滑了=.=,掉到了一个洞穴里,当他醒来时,发现自己居然落进了一个地下迷宫(真够背的),而牧师所处的这个密室周围有三道门,还好,不是三百道,还有希望,于是,牧师就开始想,该怎么出去呢?又没什么线索,难道要靠运气吗?唉~,想起运气,牧师慢慢闭上了自己的双眼,回忆起自己昨天的经历——跟一群
三岁小孩子玩五分钱一局的掷色子游戏,硬是输了400多块,而自己正是因为这件事,才到森林散步,可没想到…。唉,往事历历在目,牧师又深深叹了一口气,他深知自己的脸有多黑,知道好运从不眷顾他,但当下,得赶紧想办法,家人还等着他回家吃饭,必须得赶快出去,既然自己走不了捷径,那么就做一次莽夫,把所有的路给走一遍,就不信出不去,说干就干,他抓起一把石子,每个门口放一粒石子,走进了第一道门,捡起石子,进入到另一个密室,发现周围还是三道门,再放石子,走第一道门(捡石子),发现是个死胡同,然后回头走第二道(捡石子),还是个死胡同,第三道也是,于是他退回到前一个密室,走进了第二道门…就这样,牧师按顺序,一条路一条路的走,走过就把石子给捡起来,遇到死胡同就掉头,就这样,不到两个小时,牧师终是找到了出口。而这,就是回溯的思想。

1.算法框架
对于搜索和回溯,有比较现成的两个框架供大家参考:
框架一:
int Search(int k)
{
for (i=1;i<=算符种数;i++)
if (满足条件)
{
保存结果
if (到目的地) 输出解;
else Search(k+1);
恢复:保存结果之前的状态{回溯一步}
}
}
框架二:
int Search(int k)
{
if (到目的地) 输出解;
else
for (i=1;i<=算符种数;i++)
if (满足条件)
{
保存结果;
Search(k+1);
恢复:保存结果之前的状态{回溯一步}
}
}
3.例题分析—全排列
【题目描述】
输出自然数 1到 n 所有不重复的排列,即 n的全排列,要求所产生的任一数字序列中不允许出现重复的数字。
【输入描述】
一个整数n
【输出描述】
由 1∼n 组成的所有不重复的数字序列,每行一个序列。每个数字之间用两个空格隔开
【样例输入】
3【样例输出】
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1【分析】
(1)题目比较典型,不要用暴力穷举做
(2)再某一轮中,用过的数不能再出现(剪枝)
(3)要判断一下是不是填满了,填满了就输出一下。
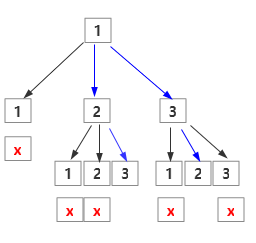
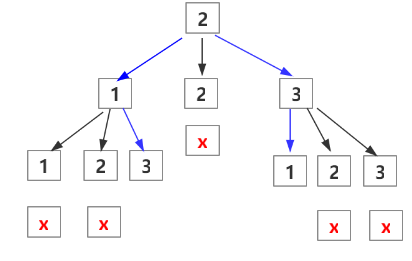
【解题思路1】
(1)定义两个数组,一个用来存放题目答案的,一个用来标记某个数在某一轮中是否被使用过。
(2)写一个输出函数,一旦填满了数就直接输出。
(3)在循环中先判断填的数是否用过,如果没有就填入,搜索下一格。
【参考代码1—框架二结构】
int Search(int k)
{
if (到目的地) 输出解;
else
for (i=1;i<=算符种数;i++)
if (满足条件)
{
保存结果;
Search(k+1);
恢复:保存结果之前的状态{回溯一步}
}
}
#include<bits/stdc++.h>
using namespace std;
int n,pd[100],ans[100];//pd数组是判断是否用过这个数,ans是结果数组
void print() { //输出函数
int i;
for(i=1; i<=n; i++)
printf("%2d",ans[i]);//保留位常宽
cout<<endl;
}
void dfs(int k) { //深搜函数,当前是第k格
int i;
if(k==n) { //填满了的时候
print();//输出当前解
return;
}
for(i=1; i<=n; i++) { //1-n循环填数
if(pd[i]==0) { //如果当前数没有用过
pd[i]=1;//标记一下,1表示当前这个数字使用过
ans[k+1]=i;//把这个数填入结果数组
dfs(k+1);//填下一个
pd[i]=0;//回溯
}
}
}
int main() {
cin>>n;
dfs(0);//注意,这里是从第0格开始的!
return 0;
}
问题1:为什么dfs要同0开始,从1开始行不行?
问题2:为什么是ans[k+1]=i?
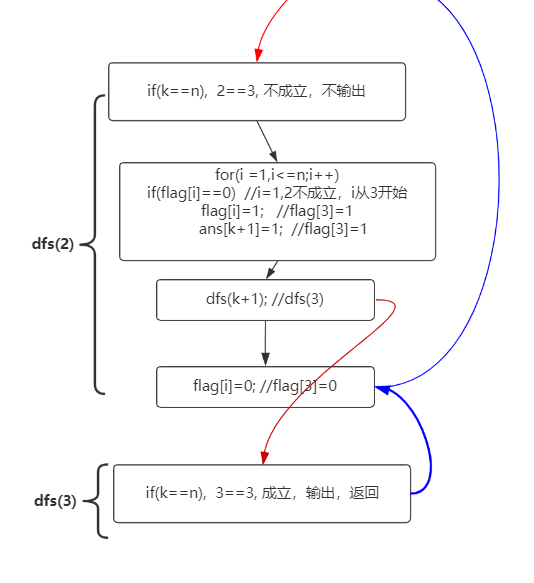
【过程分解】
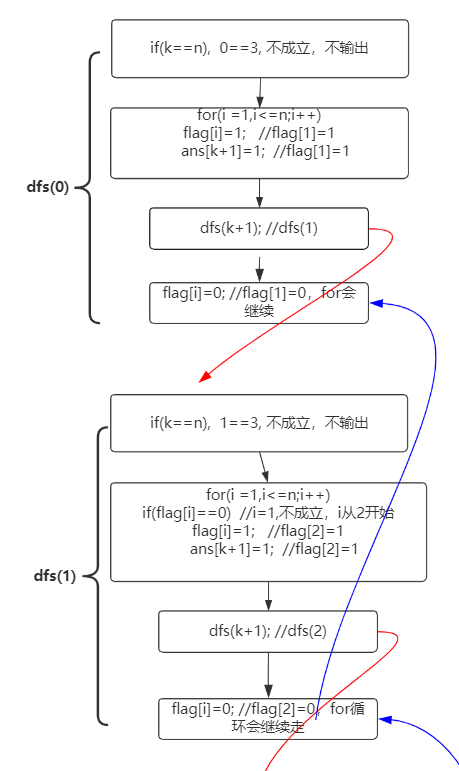
【参考代码2—框架一结构】
int Search(int k)
{
for (i=1;i<=算符种数;i++)
if (满足条件)
{
保存结果
if (到目的地) 输出解;
else Search(k+1);
恢复:保存结果之前的状态{回溯一步}
}
}
#include<cstdio>
#include<iostream>
#include<iomanip>
using namespace std;
int ans[10001]={0},n; //存放答案的数组
bool flag[10001]={0}; //标记这个数有没有被使用过,0表示没有使用
int print()
{
for (int i=1;i<=n;i++)
cout<<setw(3)<<ans[i];
cout<<endl;
}
int search(int k)
{
int i;
for (i=1;i<=n;i++) //1到n开始枚举
if(flag[i]==0) //如果当前这个数没有使用过
{
ans[k]=i; //把当前这个数放到结果数组中
flag[i]=1; //把当前数标记为使用过
if (k==n) print(); //如果枚举到边界,直接输出
else search(k+1); //否则,继续枚举下一个位置。
flag[i]=0; //回溯一步
}
}
int main()
{
cin>>n;
search(1); //从第一个位置开始
}
返回目录:算法