一、基础版排队打水
【题目描述】
学校里有一个水房,水房里一共装有m 个龙头可供同学们打开水,每个龙头每秒钟的供水量相等,均为1。
现在有n 名同学准备接水,他们的初始接水顺序已经确定。将这些同学按接水顺序从1到n 编号,i号同学的接水量为wi。接水开始时,1到m 号同学各占一个水龙头,并同时打开水龙头接水。当其中某名同学j完成其接水量要求wj后,下一名排队等候接水的同学k马上接替j 同学的位置开始接水。这个换人的过程是瞬间完成的,且没有任何水的浪费。即j 同学第x 秒结束时完成接水,则k同学第x+1 秒立刻开始接水。若当前接水人数n′不足m,则只有n′个龙头供水,其它m−n′个龙头关闭。
现在给出n名同学的接水量,按照上述接水规则,问所有同学都接完水需要多少秒。
二、进阶版排队打水
【题目描述】
有n个人排队到r个水龙头去打水,他们装满水桶的时间t1,t2,…,tn为整数且各不相等,应如何安排他们的打水顺序才能使他们总共花费的时间最少?
【输入描述】
第一行n,r (n<=500,r<=75)
第二行为n个人打水所用的时间Ti (Ti<=100);
【输出描述】
最少花费时间
【样例输入1】
3 2
1 2 3
【样例输出1】
7【样例输入2】
4 2
2 6 4 5【样例输出2】
23【题目分析】
(1)题目描述比较坑,有一个非常重要的点没有告知:
接水的总时间=每个人接水的时间之和
每个人接水花费的时间=每个人接水的时间+等待时间
(2)我们是已经知道了每个人的接水的时间,现在的主要目的是如何给他们排队,让总时间最少。
样例1的解释,一共3个人,2个水龙头。
策略一:先让花费时间最少的两个人先去。
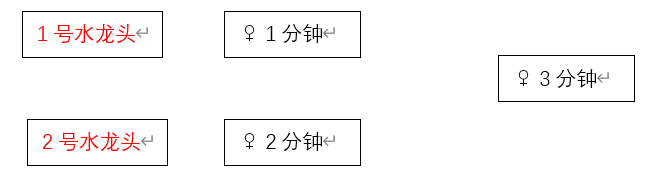
这里第一名同学需要花费了1分钟,第二名同学需要花费了2分钟。此时第三位同学还没有安排,但是已知第三名同学接水需要3分钟,如果第三位同学在2号水龙头,那么他将花费3+2(2是他在2号水龙头等待的时间),比他在1号水龙头额外多花1分钟。显然,3号同学应该在1号水龙头后等待接水,这样总体接水的时间是最少的。
1+2+(3+1)=7
策略二:让花费时间的多的先去。
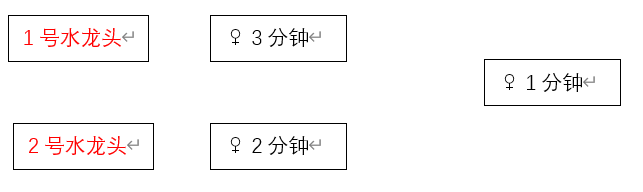
我们让花费时间最多的两位同学先去,这个时候,最后一位同学有如果在2号水龙头,他将花费2+1分钟。如果去1号水龙头,他将花3+1分钟。显然,在策略二中最少的排队接水时间应该是3+2+(2+1)=8分钟。
综上来说,对于样例1,应该选择策略一,将需要排队人总是安排到当前水龙头花费时间最少的那个。
同样,样例2,也可以有类似的解释。
(3)我们要求一个总时间,某个人的花费时间是排在当前这个水龙头的总时间+ 这个人接水的时间。
【参考代码1】
#include<cstdio>
#include <algorithm>
using namespace std;
int water[501]; //学生接水时间数组
int taps[501]= {0}; //水龙头
int main() {
int n,r;
int sum=0;
scanf("%d%d",&n,&r);
int i;
for(i=0; i<n; i++)
scanf("%d",&water[i]);
sort(water,water+n); //让接水时间短的先接水
for(i=0; i<n; i++) { //每次循环一个人
sort(taps,taps+r); //r水龙头,找出当前时间哪个水龙头接水时间最短
sum+=taps[0]+water[i]; //taps[0]肯定是接水时间最短的那个队的总时间,让当前这个人去这个队
taps[0]+=water[i]; //把当前这个人接水时间加到当前水龙头里
}
printf("%d\n",sum);
return 0;
}
对于测试数据
4 2
2 6 4 5的过程表示是

排队打水的数学推导过程
要让平均排队时间最小,就要让打水快的人往前排
证:
设有n个人打水,每个人的打水时间分别为 x_1,x_2,x_2,…,x_nx1,x2,x2,…,xn
则打水时间总和为x_1*(n-1)+x_2*(n-2)+…+x_{n-1}*1+x_n*0x1∗(n−1)+x2∗(n−2)+…+xn−1∗1+xn∗0
要让打水总时间最小,就要让x_1<x_2<…<x_nx1<x2<…<xn
所以我们可得
1.排序,对输入进行排序,使其变成x_1<x_2<…<x_nx1<x2<…<xn这个序列
2.累加时间,如果用x_1*(n-1)+…+x_{n-1}*1+x_n*0x1∗(n−1)+…+xn−1∗1+xn∗0会比较麻烦,我们换一个方式,令x_0=0x0=0 我们求x_0+(x_0+x_1)+…+(x_0+x_2+…+x_{n-1})x0+(x0+x1)+…+(x0+x2+…+xn−1)
3.把加完的时间除以n,再把x_1,x_2,…,x_nx1,x2,…,xn和时间输出
总等待时间:t1+(t1+t2)+(t1+t2+t3)+……+(t1+t2+t3+……+tn)
所以要把接水时间较少的放在前面
三、相关题目
【题目描述】
有n个人在一个水龙头前排队接水,假如每个人接水的时间为Ti,请找出这n个人排队的一种顺序,使得n个人的平均等待时间最小。
【输入描述】
第一行为一个整数n。第二行n个整数,第i个整数Ti表示第i个人的等待时间Ti。
【输出描述】
输出有两行,第一行为一种平均等待时间最短的排队顺序;第二行为这种排队方法下的平均等待时间。(结果保留小数点后两位)
【样例输入】
10
56 12 1 99 1000 234 33 55 99 812【样例输出】
3 2 7 8 1 4 9 6 10 5
291.90返回目录:算法