- 单项选择题 (共20题,每题1.5分,共计30分。每题有且仅有一个正确答案。)
1. 2E+03 表示(D )
A. 2.03 B. 5 C. 8 D. 2000
【解析】科学计数法,就是2 * 10 的3次方,答案选D
2.一个字节( byte )由(A)个二进制位组成
A. 8 B. 16 C. 32 D. 以上都有可能
【解析】 1 byte = 8 bit
3.以下逻辑表达式的值恒为真的是(A)
A. P∨(┐P ∧Q) ∨(┐P∧┐Q) B. Q∨ (┐P∧Q) ∨(P∧┐Q)
C. P∨Q∨(P∧┐Q) ∨(┐P ∧Q) D. P∨ ┐Q∨(P ∧┐Q) ∨(┐P∧┐Q)
【解析】
且或非的真值表
| p | q | p∧q(且) | p∨q(或) | ┐p(非) | ┐q |
| 真 | 真 | 真 | 真 | 假 | 假 |
| 真 | 假 | 假 | 真 | 假 | 真 |
| 假 | 真 | 假 | 真 | 真 | 假 |
| 假 | 假 | 假 | 假 | 真 | 真 |
总结:一真或为真,一假且为假
此题P,Q没有值,所以需要分类讨论P,Q的值是多少。
A项:假设P,Q都是真,则┐P ∧Q为真,┐P∧┐Q 为假, P(真)∨真∨假结果为真。
假设P为真,Q为假,则┐P ∧Q为假,┐P∧┐Q为假,P(真)∨假∨假结果为真。
假设P为假,Q为真,则┐P ∧Q为真,┐P∧┐Q为假,P(假)∨真∨假结果为真。
假设P为假,Q为假,则┐P ∧Q为假,┐P∧┐Q为真,P(假)∨假∨真结果为真。
B项:假设P,Q都为真,则┐P∧Q为假,P∧┐Q为假,Q(假)∨假∨假结果为假。
C项:假设P, Q都为真,则P∧┐Q为假,┐P ∧Q为假,P(真)∨Q(真)∨假∨假 结果为真。
假设P为真,Q为假,则P∧┐Q为真,┐P ∧Q为假,P(真)∨Q(假)∨真∨假 结果为真。
假设P为假,Q为真,则P∧┐Q为假,┐P ∧Q为真,P(假)∨Q(真)∨假∨真 结果为真
假设P为假,Q为假,则P∧┐Q为假,┐P ∧Q为假,P(假)∨Q(假)∨假∨假 结果为假
D项:假设P,Q为真,则P ∧┐Q为假,┐P∧┐Q为假,P(真)∨┐Q(假) ∨假∨假 结果为真。
假设P为真,Q为假,则P∧┐Q为真,┐P∧┐Q为假,P(真)∨┐Q(真) ∨真∨假 结果为真。
假设P为假,Q为真,则P∧┐Q为假,┐P∧┐Q为假,P(假)∨┐Q(假) ∨假∨假 结果为假。
实际上,通过观察选项可以知道,最终进行判断的都是或条件,也就是说,中间的表达式只有一个为真,那么结果就为真了。必须是所有的表达式为假最终结果才能是假。
4.Linux 下可执行文件的默认扩展名为( D)
A. exe B. com C. dll D. 以上都不是
【解析】
A项:exe是windows下的可执行程序的后缀。
B项:com是网站的后缀,一般表示公司类网站
C项:DLL是动态链接库,DLL是一个包含可由多个程序,同时使用的代码和数据的库
D项:Linux与Windows不同,不是根据扩展名来区分文件类型的。事实上,Linux下的文件不需要扩展名。一切皆文件,包含设备文件、目录文件、普通文件等。要知道是否是可执行文件,一般是通过 ls -l 命令看文件属性中是否包含可执行权限 (x)
5.如果树根算第 1 层,那么一棵 n 层的二叉树最多有( A)个结点
A. 2n-1 B. 2 n C. 2 n +1 D. 2 n+1
【解析】
考察二叉树的性质。
性质1:在二叉树的第i层,最多有2i-1个结点(i>=1)
性质2:深度为k的二叉树,至多有2K-1个结点(K>=1)
6.提出“存储程序”的计算机工作原理的是(D )
A. 克劳德·香农 B. 戈登·摩尔 C. 查尔斯·巴比奇 D. 冯·诺依曼
【解析】
A项:提出熵的概念,信息论的开创者
B项:摩尔定律的创始人,世界头号CPU生产商Intel公司的创始人之一
C项:查尔斯·巴比奇被称为现代计算机的鼻祖。提出了差分机与分析机的设计概念
D项:在现代计算机、博弈论、核武器和生化武器等领域内的科学全才之一,被后人称为“现代计算机之父”、“博弈论之父”,提出存储程序和程序控制
7.设 X、Y、Z 分别代表三进制下的一位数字,若等式 XY + ZX = XYX 在三进制下成立, 那么同样在三进制下,等式 XY * ZX = ( B)也成立。
A. YXZ B. ZXY C. XYZ D. XZY
【解析】
三进制的三个数字分别为0,1,2。X,Y,Z使用这三个数字测试
X Y
Z X
——-
X Y X
上式是两位数加两位数,可知有进位,可以知进位X的值为1,不可能为2。同时由Y+X=X可知,只有0+1=1,0+2=2符号情况。那么Y是0。根据X+Z=Y知,Z应该是2。计算XY*ZX,则计算10*21。结果为210,对应的是ZXY。
8.Pascal 语言、 C 语言和 C++ 语言都属于(D )
A. 面向对象语言 B. 脚本语言 C. 解释性语言 D. 编译性语言
【解析】
面向对象语言:Java,C++,C#,python
脚本语言: PHP, VBScript, HTML, PowerShell,JavaScript
解释性语言: 程序不需要编译,程序在运行时才翻译成机器语言,每执 行一次都要翻译一次.,例如JavaScript、VBScript、Perl、Python、Ruby、MATLAB
编译性语言: 程序在执行之前需要一个专门的编译过程,把程序编译成 为机器语言的文件,运行时不需要重新翻译,直接使用编译的结果就行了。C/C++、Pascal/Object Pascal(Delphi)
9. 前缀表达式“ + 3 * 2 + 5 12 ”的值是(C )
A. 23 B. 25 C. 37 D. 65
【解析】
前缀转中缀表达式方法:①画二叉树,②堆栈法,③加括号法。
主要介绍第二种。规则如下:
- 从右至左扫描表达式,如果遇到操作数,则入栈。
- 如果遇到操作符,则将栈顶元素弹出(后扫面的数字位于表达式前面),并和操作符结合写成表达式,作为中缀表达式再次入栈。
- 如果遇到的操作符优先级大于已存在表达式的最后执行操作符的优先级,则将已存在的表达式加上括号。
- 注意计算顺序,一般栈顶的元素在前。
| 操作符 | 说明 | 栈内情况(栈底->栈顶) | |
| 12 | 数字,入栈 | 12 | |
| 5 | 数字,入栈 | 12 | 5 |
| + | 操作符,计算栈顶两个元素,并把计算结果再次入栈。 | 5+12 | |
| 2 | 数字,入栈 | 5+12 | 2 |
| * | 操作符,计算栈顶两个元素。并把计算结果再次入栈。栈顶元素在前,所以要加括号。 | 2*(5+12) | |
| 3 | 数字,入栈 | 2*(5+12) | 3 |
| + | 操作符,计算栈顶两个元素。并把计算结果再次入栈。 | 3+2*(5+12) | |
| 空 | 没有操作符,输出 |
计算3+2*(5+12)结果为37。
10.主存储器的存取速度比中央处理器( CPU)的工作速度慢得多, 从而使得后者的效率受 到影响。 而根据局部性原理, CPU所访问的存储单元通常都趋于聚集在一个较小的连续区域 中。于是,为了提高系统整体的执行效率,在 CPU中引入了(B )。
A. 寄存器 B. 高速缓存 C. 闪存 D. 外存
【解析】
A项:寄存器是中央处理器内的组成部分。寄存器是有限存贮容量的高速存贮部件,它们可用来暂存指令、数据和位址。
B项:高速缓冲存储器是存在于主存与CPU之间的一级存储器, 由静态存储芯片(SRAM)组成,容量比较小但速度比主存高得多(属于高速缓存), 接近于CPU的速度。
C项:闪存是技术人员保存安装BIOS等计算机基础设置的地方,也可以是数码相机内的数据存储卡,不属于CPU的范畴
D项:外存是是指除计算机内存及CPU缓存以外的储存器,此类储存器一般断电后仍然能保存数据。常见的外存储器有硬盘、软盘、光盘、U盘等。
11.一个字长为 8 位的整数的补码是 11111001 ,则它的原码是(D )
A. 00000111 B. 01111001 C. 11111001 D. 10000111
【解析】
一个正数的原码=反码=补码,一个负数的原码=补码取反加1,本题“1111 1001”首位数是“1”,则这个数是负数,则原码=补码取反码加1=1000 0110=1000 0111,故选D
12.基于比较的排序时间复杂度的下限是(B ),其中 n 表示待排序的元素个数。
A. O(n) B. O(n log n) C. O(log n) D. O(n 2 )
【解析】
对于排序的按是否比较分为比较类和非比较类。
比较类有:交换(冒泡、快排),插入(简单插入、希尔),选择(简单选择,堆排),归并(二路归并,多路归并)
非比较类:计数排序,桶排序,基数排序
对于n个待排序元抄素,在未比较时,可能的正确结果有n!种。这些序列都是右面这个二叉树中某一个从根到叶子的路径。那么基于比较的排序的时间复杂度就是这颗数的深度H(N)。而且很容易知道叶子节点的个数就是N的排列 N!,那么我们就有
比属较次数至少为log(N!)=O(NlogN)(斯特林公式)。
注:斯特林公式(Stirling’s approximation)是一条用来取n的阶乘的近似值的数学公式
13. 一个自然数在十进制下有 n 位,则它在二进制下的位数与( B)最接近。
A. 5n B. n*log 210 C. 10*log 2n D. 10 nlog 2n
【解析】
十进制转二进制一般使用除二取余法。
可以举例尝试,
两位数37,转换成二进制是100101
A项:5*2=10
B:项 n*log 210≈6.64
C项: 10*log 2n=10
D项:10 nlog 2n =100
再如:三位数176,转换成二进制是10110000
A项:5*3=15
B:项:n*log 210≈10.53
C项: 10*log 2n≈15.8
D项:10 nlog 2n =1584.96
没有好的证明方法,通过举例可以看出,B项是最接近的。
14.在下列 HTML 语句中,可以正确产生一个指向 NOI 官方网站的超链接的是( B)
A. <a url=“http://www.noi.cn”>欢迎访问NOI网站</a>
B. <a href=“http://www.noi.cn”>欢迎访问NOI网站</a>
C. <a> http://www.noi.cn</a>
D. <a name=“http://www.noi.cn”>欢迎访问NOI网站</a>
【解析】
在HTML 中超链接的标签是 a。a的用法是 <a> “要显示的内容”</a> 。href表示这个超链接指向的地址是什么地方。
15.元素 R1、R2、R3、R4、R5 入栈的顺序为 R1、R2、R3、R4、R5。如果第 1 个出栈的 是 R3,那么第 5 个出栈的不可能是(B )。
A. R1 B. R2 C. R4 D. R5
【解析】
只说了入栈顺序,没有具体说出栈顺序。
入栈顺序:R1,R2, R3。因为R3第一个出栈,所以R4和R5此时不能入栈,必须等R3先出栈。当R3出栈后,栈内还剩R1,R2,观察可以看出,R2在R1的上面,不论怎样R2一定比R1先出栈,最坏的情况是R1最后出栈,所以选B
16.双向链表中有两个指针域 llink 和 rlink ,分别指向该结点的前驱及后继。 设 p 指向 链表中的一个结点,它的左右结点均非空。现要求删除结点 p ,则下面语句序列中错误的是 (A )。
A. p->rlink->llink = p->rlink; p->llink->rlink = p->llink; delete p;
B. p->llink->rlink = p->rlink; p->rlink->llink = p->llink; delete p;
C. p->rlink->llink = p->llink; p->rlink->llink->rlink = p->rlink; delete p;
D. p->llink->rlink = p->rlink; p->llink->rlink->llink = p->llink; delete p;
【分析】
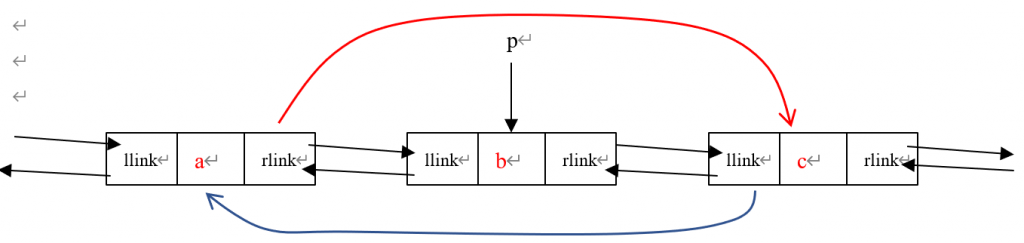
步骤:(思路:断开连接,再删除)
第一步:找到即将被删除的节点 p
第二步:将 p 的前驱的后继指向 p 的后继,即 p->rlink->llink = p->rlink;
第三步:将 p 的后继的前驱指向 p 的前驱,即 p->llink->rlink = p->llink;
第四步:删除节点 p 即 delete p;
17.一棵二叉树的前序遍历序列是 ABCDEFG,后序遍历序列是 CBFEGDA,则根结点的左 子树的结点个数可能是( A)。
A. 2 B. 3 C. 4 D. 5
【解析】
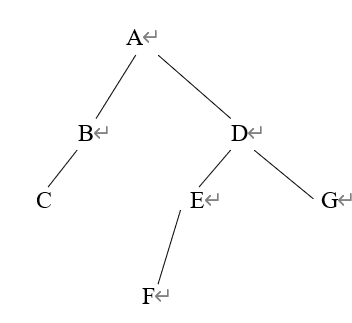
已知前序遍历和后续遍历不能确定唯一一棵二叉树
先序遍历是先访问根结点,再从左到右按照先序思想遍历各个子树
后序遍历是从左到右遍历各个子树,再访问跟结点。
可以画出如上图所示的图像。
18.关于拓扑排序,下面说法正确的是(D )。
A. 所有连通的有向图都可以实现拓扑排序
B. 对同一个图而言,拓扑排序的结果是唯一的
C. 拓扑排序中入度为 0 的结点总会排在入度大于 0 的结点的前面
D. 拓扑排序结果序列中的第一个结点一定是入度为 0 的点
【解析】
拓扑排序:对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
A项:当图中有环时,必然无法拓扑排序
B项:同一时刻,入度为0的点不唯一,拓扑排序也就不唯一
C项:可以举例说明,如
1->3
2
也是正确的拓扑排序,当时3却在2之前
19. 完全二叉树的顺序存储方案,是指将完全二叉树的结点从上至下、从左至右依次存放 到一个顺序结构的数组中。假定根结点存放在数组的 1 号位置,则第 k 号结点的父结点如 果存在的话,应当存放在数组的(C )号位置。
A. 2k B. 2k+1 C. ⌊k/2⌋ D. ⌊(k+1)/2⌋
【解析】
对于k=1,则k为根结点,无父母结点。
对于k>1,可分两种情况讨论。
1. 设完全二叉树第j层的百第一个结点的编号为i,则i=2的j-1次方。其度左孩子必为第j+1层的第一个结点。其编号为2的j次方,这和2*i相等。右孩子为j+1层的第二个结点,结点编号为2*i+1。所以,在这种情况下,左孩子编号为2*i,右孩子编号为2*i+1,父母结点编号为i,2*i/2,(i*2+1)/2取整均为i。
2. 设完全二叉树第回j层上的某个结点编号为i,编号为i+1的结点为编号为i的结点的右兄弟或者堂兄弟,若它有左孩子,编号为2i+2=2(i+1),或它有右孩子,编号为2i+3=2(i+1)+1。在答这种情况下,2(i+1)/2,[2(i+1)+1]/2取整均为i+1。
实际上,稍微寻找一下规律便知道,当k是偶数,父结点是k/2, 当k是奇数,父结点是(k-1)/2,综合一下就是k/2 向下取整。
20 .全国青少年信息学奥林匹克系列活动的主办单位是(D )。
A. 教育部 B. 科技部 C. 共青团中央 D. 中国计算机学会
【解析】
常识题,举办的单位是中国计算机协会(CCF)
二、问题求解(共 2 题,每题 5 分,共计 10 分)
1.LZW 编码是一种自适应词典编码。在编码的过程中,开始时只有一部基础构造元素的编 码词典, 如果在编码的过程中遇到一个新的词条, 则该词条及一个新的编码会被追加到词典 中,并用于后继信息的编码。 举例说明,考虑一个待编码的信息串: “xyx yy yy xyx” 。初始词典只有 3 个条目, 第一个为 x,编码为 1;第二个为 y,编码为 2 ;第三个为空格,编码为 3;于是串 “xyx” 的编码为 1-2-1 (其中 – 为编码分隔符) ,加上后面的一个空格就是 1-2-1-3 。但由于有了 一个空格, 我们就知道前面的 “xyx” 是一个单词, 而由于该单词没有在词典中, 我们就可以 自适应的把这个词条添加到词典里,编码为 4 ,然后按照新的词典对后继信息进行编码,以 此类推。于是,最后得到编码: 1-2-1-3-2-2-3-5-3-4 。 现在已知初始词典的 3 个条目如上述,则信息串 “yyxy xx yyxy xyx xx xyx” 的 编码是 2-2-1-2-3-1-1-3-4-3-1-2-1-3-5-3-6 或22123113431213536。
【解析】
LZW是一种编码是一种字典编码。其基本原理是把没见过的按顺序编号都放入字典中。
流程图:
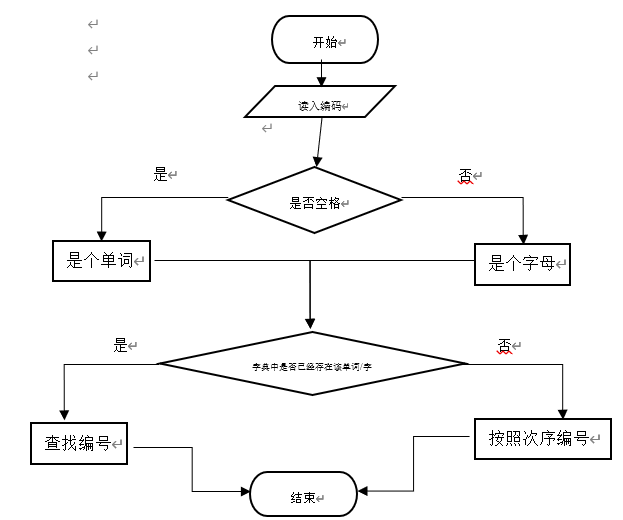
题目中的样例解释
| 信息串 | 字典里的编号 | 说明 |
| x | 1 | 第一个字符,编号为1 |
| y | 2 | 第二个字符,编号为2 |
| x | 1 | x出现过一次,查找编号,编号为1 |
| 空格 | 3 | 空格字符,编号为3 |
| xyx | 4 | 遇到空格,前面的作为一个单词,编到字典里 |
| y | 2 | y出现过一次,查找编号,编号为2 |
| y | 2 | y出现过一次,查找编号,编号为2 |
| 空格 | 3 | 空格字符,出现过,编号为3 |
| yy | 5 | 遇到空格,前面的作为一个单词,编到字典里 |
| y | 2 | y出现过一次,查找编号,编号为2 |
| y | 2 | y出现过一次,查找编号,编号为2 |
| 空格 | 3 | 空格字符,出现过,编号为3 |
| yy | 5 | 遇到空格,查找单字典里有单词,编号为5 |
| x | 1 | 第一个字符串,编号为1 |
| y | 2 | 第二个字符串,编号为2 |
| x | 1 | x出现过一次,查找编号,编号为1 |
| 空格 | 3 | 空格字符,编号为3 |
| xyx | 4 | 遇到空格,查找单字典里有单词,编号为4 |
样例的结果为1-2-1-3-2-2-3-5-3-4,也就是说,单词第一次出现只编号放入到字典中,第二次出现直接显示编号即可。而且最后一个空格不输出。
则yyxy xx yyxy xyx xx xyx应该有如下过程:(题目中已经说明有以上条目,x为1,y为2,空格为3)
| 信息串 | 字典里的编号 | 说明 | 结果序列 |
| y | 2 | 遵循题目要求,y初始为2 | 2 |
| y | 2 | y为2 | 2-2 |
| x | 1 | x初始为1 | 2-2-1 |
| y | 2 | 2-2-1-2 | |
| 空格 | 3 | 遇到空格,空格为3 | 2-2-1-2-3 |
| yyxy | 4 | 按照顺序编号,则yyxy这个单词为4 (只编号,不显示) | 2-2-1-2-3 |
| x | 1 | 出现过 | 2-2-1-2-3-1 |
| x | 1 | 出现过 | 2-2-1-2-3-1-1 |
| 空格 | 3 | 2-2-1-2-3-1-1-3 | |
| xx | 5 | xx做为一个单词,没有出现过,编号为5(只编号不,显示) | 2-2-1-2-3-1-1-3 |
| yyxy | 4 | 出现过 | 实际上是单词的一部分 |
| 空格 | 3 | 空格,前方是一个单词,是4,然后再加上空格3 | 2-2-1-2-3-1-1-3-4-3 |
| x | 1 | 出现过 | 2-2-1-2-3-1-1-3-4-3-1 |
| y | 2 | 出现过 | 2-2-1-2-3-1-1-3-4-3-1-2 |
| x | 1 | 出现过 | 2-2-1-2-3-1-1-3-4-3-1-2-1 |
| 空格 | 3 | 空格 | 2-2-1-2-3-1-1-3-4-3-1-2-1-3 |
| xyx | 6 | xyx是一个新单词,编号为6,(只编号,不显示) | |
| xx | 1 | 出现过 | 2-2-1-2-3-1-1-3-4-3-1-2-1-3-5 |
| 空格 | 3 | 空格 | 2-2-1-2-3-1-1-3-4-3-1-2-1-3-5-3 |
| xyx | 6 | 出现过 | 2-2-1-2-3-1-1-3-4-3-1-2-1-3-5-3-6 |
| 空格 | 最后一个不输出 |
2.队列快照是指在某一时刻队列中的元素组成的有序序列。例如,当元素 1 、2 、3 入队, 元素 1 出队后, 此刻的队列快照是 “2 3” 。当元素 2、3 也出队后,队列快照是 “” ,即为空。 现有 3 个正整数元素依次入队、出队。已知它们的和为 8,则共有 ___49______ 种可能的不 同的队列快照(不同队列的相同快照只计一次)。例如, “5 1″ 、”4 2 2″ 、”” 都是可能 的队列快照;而 “7” 不是可能的队列快照,因为剩下的 2 个正整数的和不可能是 1。
【解析】
三个正整数和为8,考虑不同的情况:
| 1 1 6 | 1 2 5 | 1 3 4 | 1 4 3 | 1 5 2 | 1 6 1 |
| 2 1 5 | 2 2 4 | 2 3 2 | 2 4 2 | 2 5 1 | |
| 3 1 4 | 3 2 3 | 3 3 2 | 3 4 1 | ||
| 4 1 3 | 4 2 2 | 4 3 1 | |||
| 5 1 2 | 5 2 1 | ||||
| 6 1 1 |
可以看出只有21个快照,然后把队头去掉
| 1 6 | 2 5 | 3 4 | 4 3 | 5 2 | 6 1 |
| 1 5 | 2 4 | 3 2 | 4 2 | 5 1 | |
| 1 4 | 2 3 | 3 2 | 4 1 | ||
| 1 3 | 2 2 | 3 1 | |||
| 1 2 | 2 1 | ||||
| 1 1 |
可以看出,上面的队列一共有21个。再次去掉队头,
| 6 | 5 | 4 | 3 | 2 | 1 |
| 5 | 4 | 2 | 2 | 1 | |
| 4 | 3 | 2 | 1 | ||
| 3 | 2 | 1 | |||
| 2 | 1 | ||||
| 1 |
去掉重复的后,还剩6个。再加上一个空最后是21+21+6+1=49
三、阅读程序写结果(共 4 题,每题 8 分,其中第 4 题( 1)、(2)各 4 分,共计 32 分)
1.
#include<iostream>
using namespace std;
void swap(int & a, int & b) {
int t;
t = a;
a = b;
b = t;
}
int main() {
int a1, a2, a3, x;
cin>>a1>>a2>>a3;
if (a1 > a2)
swap(a1, a2);
if (a2 > a3)
swap(a2, a3);
if (a1 > a2)
swap(a1, a2);
cin>>x;
if (x < a2)
if (x < a1)
cout<<x<<' '<<a1<<' '<<a2<<' '<<a3<<endl;
else
cout<<a1<<' '<<x<<' '<<a2<<' '<<a3<<endl;
else if (x < a3)
cout<<a1<<' '<<a2<<' '<<x<<' '<<a3<<endl;
else
cout<<a1<<' '<<a2<<' '<<a3<<' '<<x<<endl;
return 0;
}
输入: 91 2 20 77
输出: 2 20 77 91
【解析】
swap函数的目的是交换两个数,注意,&表示取地址符,也就是这个操作会把main函数中的值一同交换。
输出值a1=91, a2=2 , a3 =20,x=77
第一个if (a1 > a2),成立,更新值为: a1=2, a2=91 , a3 =20,x=77
第二个if (a2 > a3),成立,更新值为: a1=2, a2=20 , a3 =91,x=77
第三个if (a1 > a2),不成立,无更新,结果为: a1=2, a2=20 , a3 =91,x=77
读入x后,判断if(x < a2),不成立,执行else语句,
继续判断if (x < a3) 成立,则按顺序输出a1,a2, x, a3
2.
#include<iostream>
using namespace std;
int rSum(int j) {
int sum = 0;
while (j != 0) {
sum = sum * 10 + (j % 10);
j = j / 10;
}
return sum;
}
int main() {
int n, m, i;
cin>>n>>m;
for (i = n; i < m; i++)
if (i == rSum(i))
cout<<i<<' ';
return 0;
}
输入: 90 120
输出: 99 101 111
【解析】
可以看函数内容先找规律,sum = sum * 10 + (j % 10);是把一个数的各位取出且把上个过程中的数扩大10倍加起来,然后缩小10倍继续求。这是一个数求逆序的步骤。
或者按如下过程逐步求规律。
观察主函数中for循环 ,是从90到120,期间的条件满足一个rSum条件则输出i。
然后观察rSum函数。从90传入进去查看过程
| 参数 | while (j != 0) | sum = sum * 10 + (j % 10); | j = j / 10; | return sum |
| 90 | 成立 | 0 | 9 | |
| 成立(j为9) | 9 | 0 | 9 | |
| 91 | 成立 | 1 | 9 | |
| 成立(j为9) | 19 | 0 | 19 | |
| 92 | 成立 | 2 | 9 | |
| 成立(j为9) | 29 | 0 | 29 |
可以猜想后面的值分别是39,49,59,69,79,89,99在这些数字中,只有99是符符合要求的,所以第一个数输出99。然后看三位数的变化。
| 参数 | while (j != 0) | sum = sum * 10 + (j % 10); | j = j / 10; | return sum |
| 100 | 成立 | 0 | 10 | |
| 成立(j为10) | 0 | 1 | ||
| 成立(j为1) | 1 | 0 | 1 | |
| 101 | 成立 | 1 | 10 | |
| 成立(j为10) | 10 | 1 | ||
| 成立(j为1) | 101 | 0 | 101 | |
| 102 | 成立 | 2 | 10 | |
| 成立(j为10) | 20 | 1 | ||
| 成立(j为1) | 201 | 0 | 201 | |
| 103 | 成立 | 3 | 10 | |
| 成立(j为10) | 30 | 1 | ||
| 成立(j为1) | 301 | 0 | 301 |
从上方可以看出函数的规律
| 输入 | 输出 |
| 90 | 9 |
| 91 | 29 |
| 92 | 39 |
| … | … |
| 100 | 1 |
| 101 | 101 |
| 102 | 201 |
| 103 | 301 |
| … | … |
函数的功能也就是输入一个数,然后把这个数倒序输出。主函数中等号表示哪些数倒叙输出后和原来一样,此题实际上是在求解回文数。
3.
#include<iostream>
#include<iostream>
using namespace std;
int main() {
string s;
char m1, m2;
int i;
getline(cin, s);
m1 = ' ';
m2 = ' ';
for (i = 0; i < s.length(); i++)
if (s[i] > m1) {
m2 = m1;
m1 = s[i];
} else if (s[i] > m2)
m2 = s[i];
cout<<int(m1)<<' '<<int(m2)<<endl;
return 0;
}
输入: Expo 2010 Shanghai China
输出: 120 112
| 字符 | 空格 | ‘0’ | ‘A’ | ‘a’ |
| ASCII码 | 32 | 48 | 65 | 97 |
【解析】
先看程序代码。有两个if的比较,在比较过程中都是把比较大的值赋值出来,且第一个if有两个赋值,分别是把较大的赋值给m2,较小的赋值给m1,那么每次循环完毕后,m2总是保持最大的值,m1总是保持最小的值。然后m1和m2的值即可。
或者也可以按照以下步骤求解规律。
| i | s[i] | 比较过程 | m1 | m2 |
| 0 | E | if成立 | E | 空 |
| 1 | x | if成立 | x | E |
| 2 | p | else成立 | x | p |
| 3 | o | 没有任何成立 | x | p |
| 4 | 空格 | 没有任何成立 | x | p |
| 5 | 2 | 没有任何成立 | x | p |
| 。。。 |
后面的任何字母都没有x和p大,所以m1保留x。m2保留p,最后输出m1和m2的值即可
4.
#include<iostream>
using namespace std;
const int NUM = 5;
int r(int n) {
int i;
if (n <= NUM)
return n;
for (i = 1; i <= NUM; i++)
if (r(n - i) < 0)
return i;
return -1;
}
int main() {
int n;
cin>>n;
cout<<r(n)<<endl;
return 0;
}
(1) 输入: 7 输出: ____1_____ (4 分)
(2) 输入: 16 输出: ____4____ (4 分)
【解析】一个递归
当n小于5时,返回n,当n大于5时,进入for循环同时递归。一定要注意for循环和递归的关系。为了方便期间,先把前面的几个求出,实际上参考表格法,可以先倒序把这些值求出,在计算过程中,直接寻找即可。如果从正面开始直接循环和递归的话很容易理不清层次而出错。
r(1)=1, r(2)=2, r(3)=3, r(4)=4, r(5)=5,
r(6)的值,首先进入到for循环中,r(6)因为for循环一个没成立,最后的结果为-1
| i | if | return |
| i=1 | r(5)<0 不成立 | |
| i=2 | r(4)<0 不成立 | |
| i=3 | r(3)<0 不成立 | |
| i=4 | r(2)<0 不成立 | |
| i=5 | r(1)<0 不成立 | |
| -1 |
r(7)的值,也是进入到for循环中,因为i=1时成立,所以r(7)=1。
| i | if | return |
| i=1 | r(6)<0 成立 | 1 |
| i=2 | 不执行 | |
| i=3 | 不执行 | |
| i=4 | 不执行 | |
| i=5 | 不执行 |
r(8)的值,也是进入到for循环中, 因为i=2时成立,所以r(7)=2。
| i | if | return |
| i=1 | r(7)<0 不成立 | |
| i=2 | r(6)<0 成立 | 2 |
| i=3 | ||
| i=4 | ||
| i=5 |
可以猜想r(9)=3,r(10)=4,r(11)=5。当r(12)时,for循环中的if (r(n – i) < 0) 没有任何一个成立,r(12)=-1
至此可以看出,整个数据是1,2,3,4,5,-1的循环,所以r(16)=4。
四、完善程序(前 4 空,每空 2.5 分,后 6 空,每空 3 分,共计 28 分)
1.(哥德巴赫猜想) 哥德巴赫猜想是指,任一大于 2 的偶数都可写成两个质数之和。迄今 为止, 这仍然是一个著名的世界难题,被誉为数学王冠上的明珠。 试编写程序,验证任一大 于 2 且不超过 n 的偶数都能写成两个质数之和。
【解析】验证哥德巴赫猜想,题目中有判断质数的部分, 查看程序第一个for循环是求n以内所有的质数,并把结果放到p数组中,第二个for循环是验证大于2的不超过n的偶数能否写成两个质数之和。
#include<iostream>
using namespace std;
int main() {
const int SIZE = 1000;
int n, r, p[SIZE], i, j, k, ans;
bool tmp;
cin>>n;
r = 1;
p[1] = 2;
for (i = 3; i <= n; i++) {
① _______;
for (j = 1; j <= r; j++)
if (i % ② ______) {
tmp = false;
break;
}
if (tmp) {
r++;
③_________
}
}
ans = 0;
for (i = 2; i <= n / 2; i++) { // i=n/2 表示缩小范围,排除重复情况。
tmp = false;
for (j = 1; j <= r; j++)
for (k = j; k <= r; k++)
if (i + i == ④ _______ ) {
tmp = true;
break;
}
if (tmp)
ans++;
}
cout<<ans<<endl;
return 0;
}若输入 n 为 2010 ,则输出 ⑤ _______ 时表示验证成功,即大于 2 且不超过 2010 的偶数都 满足哥德巴赫猜想。
①【 tmp=true 】tmp初始化,因为下方出现了修改tmp的值,所以tmp为true
②【 p[j] 】判断能否整除,如果能则修改tmp的值,并直接结束掉此循环。所以这个地方是判断i是不是质数,p数组是用来存放质数的数组。
③【 p[r]=i 】r++,是准备存取下一个质数到p数组中,所以应该是p[r]=i;
④ 【 p[j]+p[k] 】此处是验证哥德巴赫猜想,大于2 的偶数可以表示成两个质数之和,所以此处应该填两个质数之和,根据上层两个for循环推出此处应该是质数的穷举,p数组的p[j]和p[k]分别穷举不同的质数组合。
⑤【 1004 】是为了表示一共有多少个需要输出。需要注意把2排除在外,所以一共2008个偶数,那么最后输出1004,因为原题范围是n/2。
2.(过河问题) 在一个月黑风高的夜晚,有一群人在河的右岸,想通过唯一的一根独木桥 走到河的左岸。 在这伸手不见五指的黑夜里, 过桥时必须借助灯光来照明, 很不幸的是,他 们只有一盏灯。 另外,独木桥上最多承受两个人同时经过,否则将会坍塌。 每个人单独过桥 都需要一定的时间,不同的人需要的时间可能不同。两个人一起过桥时,由于只有一盏灯,所以需要的时间是较慢的那个人单独过桥时所花的时间。现输入 n( 2≤n≤100)和这 n 个 人单独过桥时需要的时间,请计算总共最少需要多少时间,他们才能全部到达河的左岸。 例如,有 3 个人甲、乙、丙,他们单独过桥的时间分别为 1、 2、4,则总共最少需要 的时间为 7 。具体方法是:甲、乙一起过桥到河的左岸,甲单独回到河的右岸将灯带回,然 后甲、丙再一起过桥到河的左岸,总时间为 2+1+4=7 。
【解析】过河问题,贪心算法的一个应用,需要明确贪心策略。
其中:
max函数是返回两个数中较大的一个。
go函数难点,从左向右走和从右向左走分成。
hour数组存放的是每个人的时间。
根据main函数中pos和hour同步赋值,推算pos数组是用来记录每个元素i所处的位置是left还是right。
ans:根据if (hour[i] > ans) ans = hour[i]; 猜想ans是从右向左最长的过桥时间。
num:一般为数字,题目中只有 if (pos[i] == RIGHT) num++;与num有关,解释为有一个人在RIGHT侧,num就加一,推论num是表示在右侧的人数。
#include<iostream>
using namespace std;
const int SIZE = 100;
const int INFINITY = 10000;
const bool LEFT = true;
const bool RIGHT = false;
const bool LEFT_TO_RIGHT = true;
const bool RIGHT_TO_LEFT = false;
int n, hour[SIZE]; //存放每个人的过河时间
bool pos[SIZE];
int max(int a, int b) {
if (a > b)
return a;
else
return b;
}
int go(bool stage) {
int i, j, num, tmp, ans;
if (stage == RIGHT_TO_LEFT) {
num = 0;
ans = 0;
for (i = 1; i <= n; i++)
if (pos[i] == RIGHT) {
num++; //人数加1
if (hour[i] > ans)
ans = hour[i]; //ans保留了最长的过桥时间,
}
if ( ① __________ )
return ans;
ans = INFINITY;
for (i = 1; i <= n - 1; i++)
if (pos[i] == RIGHT) //如果这个人在右侧
for (j = i + 1; j <= n; j++)
if (pos[j] == RIGHT) {
pos[i] = LEFT;
pos[j] = LEFT;
tmp = max(hour[i], hour[j]) + ② __________) ;
if (tmp < ans)
ans = tmp;
pos[i] = RIGHT;
pos[j] = RIGHT;
}
return ans;
}
if (stage == LEFT_TO_RIGHT) {
ans = INFINITY;
for (i = 1; i <= n; i++)
if ( ③_________) {
pos[i] = RIGHT;
tmp = ④ _________;
if (tmp < ans)
ans = tmp;
⑤__________ ;
}
return ans;
}
return 0;
}
int main() {
int i;
cin>>n;
for (i = 1; i <=n; i++) {
cin>>hour[i];
pos[i] = RIGHT; //pos是记录每个元素所处的位置。
}
cout<<go(RIGHT_TO_LEFT)<<endl; //初始状态RIGHT_TO_LEFT
return 0;
}
本小题中, LEFT 可用 true 代替, LEFT_TO_RIGHT 可用 true 代替, RIGHT_TO_LEFT 可用 false 代替。
①【 num<=2 】【解析】根据go函数的内容,这部分是从右向左,下方是return ,也就是询问if满足什么条件时可以结束程序,当右边的人小于等于2时,表示右边人全部已经到左边了。
②【 go(LEFT_TO_RIGHT 】是一个普通的回溯,此次过桥的时间+未知的后续的过桥时间
③【 pos[i] == LEFT 】 跟上方类似,上一处判断是ROGHT侧,这里判断在LEFT侧。
④ 【 hour[i] + go(RIGHT_TO_LEFT) 】 此处再次递归
⑤【 pos[i] = LEFT 】 将状态改回
【附注】
题目中的例子太弱,举原例说明。
假如甲乙丙丁4人单独过河所需时间分别是1,2,5,8。那么在这种情况下,
- 第一种方案:甲乙先过去(2分钟),甲回来(1分钟),甲丙过去(5分钟),甲回来(1分钟),甲丁过去(8分钟)。总共17分钟
- 第二种方案:甲乙过去(2分钟),甲回来(1分钟),丙丁过去(8分钟),乙回来(2分钟),甲乙过去(2分钟)。总共15分钟。
可以看出这种方法的关键点,是让两个最慢的人同时过桥。
那么看下一种例子,假如甲乙丙丁过河时间分别是1,4,5,8
- 第一种方案:甲乙过去(4分钟),甲回来(1分钟),甲丙过去(5分钟),甲回来(1分钟),甲丁过去(8分钟)总共19分钟。
- 第二种方案:甲乙过去(4分钟),甲回来(1分钟),丙丁过去(8分钟),乙回来(4分钟),甲乙过去(4分钟),总共21分钟。
这次,两个最慢的人反而更慢了。上面两种方案的差异,是次快的人要不要也传递灯。
总结两种方式:
- 最快的(即所用时间t[0])和次快的过河,然后最快的回来,再次慢的和最慢的过河,然后次快的回来
- 最快的和最慢的过河,然后最快的回来,再最快的和次慢的过河,然后最快的回来。
那么,可以继续总结下思路:
- 首先明确,每次要送回去灯,这就要求送灯的人必须是他们中最快的。
- 既然送回灯的人必须是其中最快的,那么这个人一定是最后一批到达对面的人。
- 两个速度较慢的人一起过河,可以节省时间。(例如:甲乙过河各需100,两人同时过河只需100,如果分别过河需要200)
- 如果速度最快的两个人速度优势不明显,比如次快和最慢的就会出现时间反而变慢了。这个时候,可以用最快的人传递等等,方法是最快的和最慢的过去回来在和次慢一起过去
- 重复上面步骤,直到所有人都过去。
此题并未按照上述算法严格执行,此解释只做拓展。
返回目录:NOIP/CSP信息学奥赛初赛