NOIP2008年普及组初赛题目答案及解析

一、 单项选择题 （共20题，每题1.5分，共计30分。每题有且仅有一个正确答案.）。

1．微型计算机中，控制器的基本功能是（  A ）。

A. 控制机器各个部件协调工作      B. 实现算术运算和逻辑运算       

C. 获取外部信息                D. 存放程序和数据
【解析】
中央处理器CPU主要由控制器和运算器组成。
运算器：主要进行算术运算和逻辑运算。
控制器：顾名思义，主要功能就是控制，是计算机的指挥系统

2. 设A=true，B=false，C=true，D=false，以下逻辑运算表达式值为真的（  B）。    
 

A. (A∧B)∨(C∧D∨┐A) B. ((┐A∧B)∨C)∧┐D
C.(B∨C∨D)∧D∧A
D. A∧(D∨┐C)∧B

【解析】
且或非的真值表

p	q	p∧q(且)	p∨q(或)	┐p(非)	┐q
真	真	真	真	假	假
真	假	假	真	假	真
假	真	假	真	真	假
假	假	假	假	真	真

 计算规则：∧是且，∨是或，┐是非
且的两侧只要有一个是假，则结果位假，或的两侧只要有一个为真，则结果为真，非就是取反。
A选项:A∧B为false，C∧D为false，C∧D的结果与 ┐A ∨的结果是 false， 则 false跟false ∨的结果是false。
B,C,D 同理，需要按照括号顺序和规则进行计算

3. 在下列关于图灵奖的说法中，不正确的是（   C）。

A. 图灵奖是美国计算机协会于1966年设立的，专门奖励那些对计算机事业作出重要贡献的个人

B. 图灵奖有“计算机界诺贝尔奖”之称

C. 迄今为止，还没有华裔计算机科学家获此殊荣

D. 图灵奖的名称取自计算机科学的先驱、英国科学家阿兰·图灵
【解析】

图灵奖（Turing Award），全称“A.M. 图灵奖（A.M Turing Award）”，由美国计算机协会（ACM）于1966年设立，专门奖励那些对计算机事业作出重要贡献的个人。 其名称取自计算机科学的先驱、英国科学家艾伦·麦席森·图灵（Alan M. Turing）（音译为：阿兰·图灵）。 由于图灵奖对获奖条件要求极高，评奖程序又是极严，一般每年只奖励一名计算机科学家，只有极少数年度有两名合作者或在同一方向作出贡献的科学家共享此奖。因此它是计算机界最负盛名、最崇高的一个奖项，有“计算机界的诺贝尔奖”之称。
     每一年的图灵奖一般在下一年的3月下旬颁发，从1966年至2019年共73名获奖者。 按国籍分，美国学者最多，欧洲学者偶见之，华人学者目前仅有2000年图灵奖得主姚期智（现在清华大学、香港中文大学）。  据相关资料统计，截止2019年3月，美国斯坦福大学的图灵奖人数（校友或教职工）位列世界第一（27位）、美国麻省理工学院（26位）位列世界第二、美国加州大学伯克利分校（25位）位列世界第三 ；哈佛大学（14位）和卡耐基梅隆大学（13位）、普林斯顿大学（13位）分列世界第四和第五名。

4．计算机在工作过程中，若突然停电，（   C ）中的信息不会丢失。

A. ROM和RAM      B. CPU       C.ROM      D. RAM
【解析】
RAM: 是内存的意思，就像你玩的一款单机游戏一样，突然断电后，下次打开游戏需要从头开始
ROM：只读存储器，类似硬盘，就是你下载下来的东西存放的地方，断电以后重新打开，还在硬盘里。
CPU：是中央处理器，主要负责计算。如果你正在算 1+1 ，这时候突然断电，开机之后刚才算的1+1 就没了

5．完全二叉树共有2*N-1个结点，则它的叶节点数是（ B  ）。

A. N-1         B. N           C. 2*N        D. 2^N-1

【解析】
两种思路
思路一：二叉树的结点，他的度只有3种，0，1和2。（想想为啥叫二叉树）
因为是完全二叉树，所以度为1的结点只可能是0个或1个（因为完全二叉树的定义是只有最下面的两层结点小于2，）。
因为（性质3）：对于任何一棵二叉树，如果其叶结点数为N0(N0表示度为0的点也就是叶子结点),而度为2的结点为N2，则N0=N2+1，
假设度为0的点数量为x，则度为2的点数量为x-1，
当度为1的点有1个时，则  x+x-1+1 = 2*N-1，解得x=N- 1/2 （因为结点必须为整数，所以答案错误）
当度为1的点有0个时，则 x+x-1+0 = 2*N-1，解得 x= N；（符合题意）
思路二：（不要作为依据）
结点总数为偶数时：叶结点数=结点总数/2
结点总数为奇数时：叶结点数=(结点总数+1)/2
如果2N-1为偶数，则（2N-1 ）/2  的结果N-1/2 ，如果结果要为整数，则N必须是分数

如果2N-1为奇数，则（（2N-1）+1）/2  的结果为N，结果为整数。

6. 在以下各项中，（ D）不是操作系统软件。

A. Solaris      B. Linux       C. Windows Vista         D. Sybase
【解析】
A：Solaris 是Sun Microsystems研发的计算机操作系统。它被认为是UNIX操作系统的衍生版本之一。 Solaris仍旧属于私有软件。2005年6月14日，Sun公司将正在开发中的Solaris 11的源代码以CDDL许可开放，这一开放版本就是OpenSolaris。
B: linux 是一款开源操作系统,世界范围内应用非常广，很多服务器系统都是基于linux的
C:windows vista 是微软公司旗下的一款操作系统，生命周期比较短
D: 美国Sybase公司研制的一种关系型数据库系统，是一种典型的UNIX或WindowsNT平台上客户机/服务器环境下的大型数据库系统。

7．设栈S的初始状态为空，元素a，b，c，d，e，f依次入栈S，出栈的序列为b，d，f，e，c，a，则栈S的容量至少应该是（   C）。

A. 6           B. 5           C. 4            D. 3
【解析】
栈是一种先进后出的数据结构。进栈顺序是a,b,c,d,e,f。过程如下

操作	栈内	栈外
a进栈	a	空
b进栈	ab	空
b出栈	a	b
c进栈	ac	b
d进栈	acd	b
d出栈	ac	bd
e进栈	ace	bd
f进栈	acef	bd
f出栈	ace	bdf
e出栈	ac	bdfe
c出栈	a	bdfec
a出栈	空	bdfeca

可以看出，栈内最多容纳4个元素。

8. 与十进制数28.5625相等的四进制数是（D  ）。

A. 123.21       B. 131.22        C. 130.22       D. 130.21
【解析】
整数部分（除n取余法）：28/4 = 7 余 0
                       7/4 =  1 余3
                       1/4=    0余1
小数部分（乘n取整法）：0.5625 * 4 = 2.25   整数部分是2
                       0.25 *4 =1.00      整数部分是1
所以结果是：130.21 (整数部分倒序，小数部分正序)        

9. 设字符串S=”Olympic”，S的非空子串的数目是（ A）。

A. 28     B. 29       C. 16            D. 17

【解析】
1个字符的子串（7个）:”o” “l” “y” “m” “p” “i” “c”,
2个字符（6个）：”ol” “ly” “ym” “mp” “pi” “ic”.
… …
6个字符（2个）：“olympi” “lympic”
7个字符（1个）:olympic 所以：共有7+6+5+4+3+2+1=28
方法2：字串公式： n(n+1)/2 +1 。n表示你字符串的长度。最后一个加1表示加的是空串，这个题说非空字串，那么就是n(n+1) /2 结果是28

10．Web2.0是近年来互联网的热门概念之一，其核心思想是互动与分享。下列网站中，（  B ）是典型的Web2.0应用。

 A. Sina         B. Flickr          C. Yahoo            D. Google
【解析】
A:Sina 是新浪，主打新闻，视频，分享（此选项不具备时效性）
B: Flickr是一家照片视频分享网站（已被收购）
C:Yahoo搜索引擎老大哥（经营不善，已经把自己卖了）
D：Google 全球搜索引擎霸主级地位（至今还是霸主）

11． 递归过程或函数调用时，处理参数和返回地址，通常使用一种称为（ D  ）的数据结构。

A. 队列          B. 多维数组         C. 线性表             D. 栈
【解析】
在函数调用过程中形成嵌套时，则应使最后被调用的函数最先返回，递归函数执行时也是如此。例如，用递归方式求4的阶乘(以factorial(n)表示求n的阶乘)的过程如下所示：
factorial(4)=4*factorial(3)
=4*(3*factorial(2))
=4*(3*(2*factorial(1)))
=4*(3*(2*1)
=4*(3*2)
=4*6
=24
显然，要求4的阶乘，需要通过递归调用求出3的阶乘，要求出3的阶乘，必须先求出2的阶乘，依此类推，求出1的阶乘后才能得到2的阶乘，然后才能得到3和4的阶乘。该求解过程中的函数调用和返回需要满足后调用先返回的特点，因此需要使用栈结构。

12.  (2008)₁₀ + (5B)₁₆的结果是（  A ）。

A. (833)₁₆     B. (2089)₁₀      C. (4163)₈      D. (100001100011)₂
【分析】
5B 转换成十进制是5B->（0101 1011）->91。（以二进制为中间单位）

2008+91=2099，首先排除B项。
A： 833-> (100000110011) -> 2099

13. 二叉树T，已知其先根遍历是1 2 4 3 5 7 6（数字为结点的编号，以下同），中根遍历是2 4 1 5 7 3 6，则该二叉树的后根遍历是（  B ）。

A. 4 2 5 7 6 3 1           B. 4 2 7 5 6 3 1 

C. 7 4 2 5 6 3 1           D. 4 2 7 6 5 3 1
【分析】
先根（序）遍历：根结点、左子树、右子树。
中根（序）遍历：左子树，根结点，右子树。
后跟（序）遍历：左子树，右子树，根结点。
先画出出二叉树（可以尝试补0）：
①首先看先根遍历的 1 2 4 ，和中根遍历的2 4 1，说明1 是根结点，2  4 都是是左子树的一部分，剩余都是右子树一部分；
②再看先序的2 4 ，然后中根遍历 2 4 1，已知1是根结点，所以2是下面一层的根节点，4是2的右子树（图1）；
③再看先跟3 5 7 6 和中根5 7 3 6，说明3是右子树的根节点，5 7 是左子树，6是右子树（图2）
④看先序遍历 5 7 和中序遍历5 7 ，说明5是根结点，7是右子树（图3）

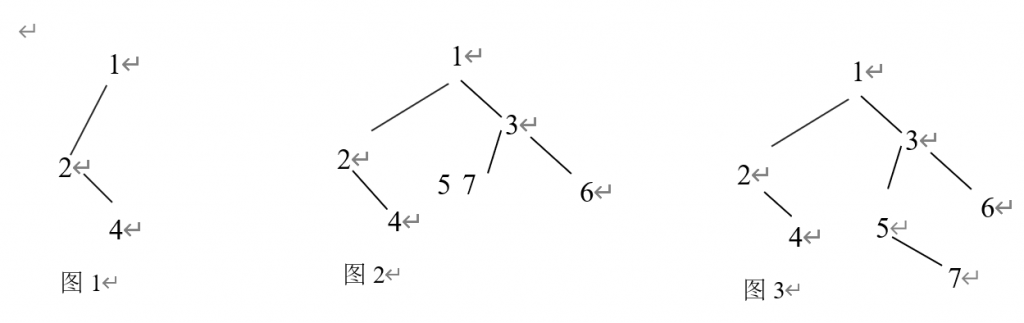
二叉树如图3所示，所以后根遍历的结果是4 2 7 5 6 3 1

14．将数组{8, 23, 4, 16, 77, -5, 53, 100}中的元素按从大到小的顺序排列，每次可以交换任意两个元素，最少需要交换（ B  ）次。

A. 4            B. 5           C. 6            D. 7
【解析】（每次从后面（未排好序的元素）选取最大的元素进行交换）
第一次交换8 和100 ：100 23 4 16 77 -5 53 8

第二次交换23和77： 100 77 4 16 23 -5 53 8

第三次交换4和53： 100 77 53 16 23 -5  4 8

第四次交换16和23：100 77 53 23 16 -5 4 8

第五次交换-5和8：100 77 53 23 16  8 4 -5

15． 对有序数组{5, 13, 19, 21, 37, 56, 64, 75, 88，92，100}进行二分查找，成功查找元素19的查找长度（比较次数）是（   B）。

A. 1            B. 2           C. 3             D. 4
【解析】
所谓二分查找通俗来讲就是一分为2，对半查找。第一次中间值是56，没有找到然后分成两部分（5，13，19，21，37）和（64，75，88，92，100）。然后对左半部分进行二分查找，中间值是19，查找成功，一共2次

16. 面向对象程序设计（Object-Oriented Programming）是一种程序设计的方法论，它将对象作为程序的基本单元，将数据和程序封装在对象中，以提高软件的重用性、灵活性和扩展性。下面关于面向对象程序设计的说法中，不正确的是（ A  ）。

A. 面向对象程序设计通常采用自顶向下设计方法进行设计。

B. 面向对象程序设计方法具有继承性（inheritance）、封装性（encapsulation）、多态性（polymorphism）等几大特点。

C. 支持面向对象特性的语言称为面向对象的编程语言，目前较为流行的有C++、JAVA、C#等。

D. 面向对象的程序设计的雏形来自于Simula语言，后来在SmallTalk语言的完善和标准化的过程中得到更多的扩展和对以前思想的重新注解。至今，SmallTalk语言仍然被视为面向对象语言的基础。
【解析】
程序设计的方法包括：结构化设计和面向对象设计方法。
不能说与面向对象相反的是什么，只能说结构化是不同于面向对象的设计方法，C和pascal都是结构化的设计方法。C++是面向对象设计方法。在结构化程序设计中采用的是自定向下、逐步求精的方法。可以说，是大问题化成小问题，逐个求解。
面向对象的三大特点：继承、封装、多态

C语言是面向过程的语言，C++、JAVA，C#等是面向对象的语言

Smalltalk是面向对象语言的基础。

17. 在32*32点阵的“字库”中，汉字“北”与“京”的字模占用字节数之和是（  B ）。

  A. 512          B.  256         C.  384          D. 128
【解析】

在32*32的点阵中，需要32*32bit = 128byte（1 byte = 8bit）
所以两个字字节数之和是256

18. 设T是一棵有n个顶点的树，下列说法不正确的是（   A ）。

A. T有n条边                     B. T是连通的

C. T是无环的                     D. T有n-1条边
【解析】
n个顶点的树，除了根结点以外，其余每个结点上方都连接一条边，所以一共有n-1条边。 

19. 下列不属于NOIP竞赛推荐使用的语言环境的是（ B  ）。

A. Dev-C++     B. Visual C++     C. free pascal      D.Lazarus

【解析】
Microsoft Visual C++（简称Visual C++、MSVC、VS或VC）是微软公司的C++开发工具，具有集成开发环境，可提供编辑C语言，C++以及C++/CLI等编程语言

Free Pascal（全称 FPK Pascal）是一个32位和64位专业Pascal编译器。

Lazarus的设计目标是应用Free Pascal，所以所有凡是Free Pascal能运行的平台，Lazarus都可以运行。

20．在C++程序中，表达式200|10的值是（  D ）

 A. 20         B. 1            C. 220         D. 202

【解析】

|表示按位或运算（规则：1|1=1     1|0=1    0|1=1     0|0=0 ）

200转换成二进制11001000

10转换成二进制00001010
11001000
 0000101

——————

    11001010   转换成十进制是202

二．问题求解（共2题，每题5分，共计10分）

1. 书架上有4本不同的书A、B、C、D。其中A和B是红皮的，C和D是黑皮的。把这4本书摆在书架上，满足所有黑皮的书都排在一起的摆法有___12__种。满足 A必须比C靠左，所有红皮的书要摆放在一起，所有黑皮的书要摆放在一起，共有___4___种摆法。

【解析】

排列组合问题，所有黑皮在一块，用捆绑法，A,B和做为一个整体的C，D、一个三个元素，所以三个元素的全排列为A(3,3)，然后解绑C，D一个两种方式，A(3,3)*2=12。
所有红皮在一块，所有黑皮在一块，用捆绑法把AB捆绑在一块，CD捆绑在一块，捆绑在一块的两个元素进行全排列，但是A必须比C靠左，所以这两个捆绑的元素只有一种排序方式，然后AB和CD分别解绑，AB解绑有A(2,2)种　,CD解绑有A(2,2)种，一共有A(2,2)*A(2,2)=4种。　
2．有6个城市，任何两个城市之间都有一条道路连接，6个城市两两之间的距离如下表所示，则城市1到城市6的最短距离为____7_________。

	城市1	城市2	城市3	城市4	城市5	城市6
城市1	0	2	3	1	12	15
城市2	2	0	2	5	3	12
城市3	3	2	0	3	6	5
城市4	1	5	3	0	7	9
城市5	12	3	6	7	0	2
城市6	15	12	5	9	2	0

【解析】

图论中的最短路径问题，使用Dijkstra算法，

【1】不断运行广度优先算法找可见点，计算可见点到源点的距离长度

【2】从当前已知的路径中选择长度最短的将其顶点加入S作为确定找到的最短路径的顶点。

7(1->2->5->6)

节点	①	②	③	④	⑤	⑥
是否标记	F	F	F	F	F	F
距离	0	0	0	0	0	0

第一步，选取开始节点①。标记为T，同时扩展与①节点有联系的节点。

节点	①	②	③	④	⑤	⑥
是否标记	T	F	F	F	F	F
距离	0	2	3	1	12	15

第二步，选取当前未被扩展的距离最小的节点④，扩展和④相关的所有节点。

节点	①	②	③	④	⑤	⑥
是否标记	T	F	F	T	F	F
距离	0	2	3	1	8	10

说明：节点④到节点②的距离是1+5大于原来的2，所以不修改。

节点④到节点⑤的距离是1+7小于原来的12，所以修改。

依次类推。

第三步, 选取当前未被扩展的距离最小的节点②，扩展和②相关的所有节点。

节点	①	②	③	④	⑤	⑥
是否标记	T	T	F	T	F	F
距离	0	2	3	1	5	10

第四步, 选取当前未被扩展的距离最小的节点③，扩展和②相关的所有节点。

节点	①	②	③	④	⑤	⑥
是否标记	T	T	T	T	F	F
距离	0	2	3	1	5	8

第五步, 选取当前未被扩展的距离最小的节点⑤，扩展和⑤相关的所有节点。

节点	①	②	③	④	⑤	⑥
是否标记	T	T	T	T	T	F
距离	0	2	3	1	5	7

结果到达⑥，最小距离就是7.

三．阅读程序写结果（共4题，每题8分，共计32分）

  

#include<iostream>
using namespace std;
int main()
{
	int i, a, b, c, d, f[4];
	for(i = 0; i < 4; i++)  cin >> f[i];
	a = f[0] + f[1] + f[2] + f[3];
	a = a / f[0];
	b = f[0] + f[2] + f[3];
	b = b / a;
	c = (b * f[1] + a) / f[2];
	d = f[(b / c ) % 4];
	if( f[(a + b + c + d) % 4]  >  f[2] )
		cout << a + b<< endl;
	else 
		cout << c + d << endl;
	return 0;
}

输入：9 19 29 39   

输出：____23_____

【解析】题目本身不难，直接模拟即可。

f[0]=9,f[1]=19,f[2]=29,f[3]=39

a= 10,b=7, c=4, d=19。  a+b+c+d =44 ,  44%4 = 0, 则f[0] = 9 和 f[2]=29 大小关系不成立，输出c+d=23

2．

#include<iostream>
using namespace std;
void foo(int a, int b, int c)
{
	if(a > b) 
		foo(c, a, b);
	else
		cout<<a<<','<<b<<','<<c<<endl;
}
int main()
{
	int a, b, c;
	cin >> a >> b >> c;
	foo(a, b, c);
	return 0;
}

输入: 3 1 2

输出: __2,3,1______

【解析】一个简单的函数递归调用

a=3,b=1,c=2。

第一次f（3，1，2），if条件成立，继续递归下一层 f（2，3，1），if条件不成立，输出结果2，3，1

3．

#include <iostream>
using namespace std;
void func(int ary[], int n )
{
	int i=0, j, x;
	j=n-1;
	while(i<j)
	{
		while (i<j&&ary[i]>0) i++;
		while (i<j&&ary[j]<0) j--;
		if (i<j){
			x=ary[i];
			ary[i++]=ary[j];
			ary[j--]=x;
		}
	}
}
int main()
{
	int a[20], i, m;
	m=10;
	for(i=0; i<m; i++)
	{
		cin>>a[i];
	}
	func(a, m);
	for (i=0; i<m; i++)
		cout<<a[i]<<" ";
	cout<< endl;
	return 0;
}

输入：5 4 -6 -11 6 -59 22 -6 1 10

输出：_5 4 10 1 6 22 -59 -6 -11 -6____

【解析】稍微复杂一点的函数调用，通过不断的给a数组赋值更新a数组的内容，比较坑的一点是ary[i++]和ary[j–]

这两个操作，a[i++] 其值等同于a[i]，然后i再自增1。 如果写a[++i],则是i先自增1再对a数组赋值。

x=ary[i];

ary[i++]=ary[j];

ary[j–]=x;

这三行代码的意思就是 交换a[i]和a[j]的值，然后i++ ,j—

PS:如果学过排序算法的话，可以想想快排的部分。那么这道题就比较简单了。如果看不透此题思想，手动模拟出错的概率很大。

纯手动模拟可以参考下面的过程

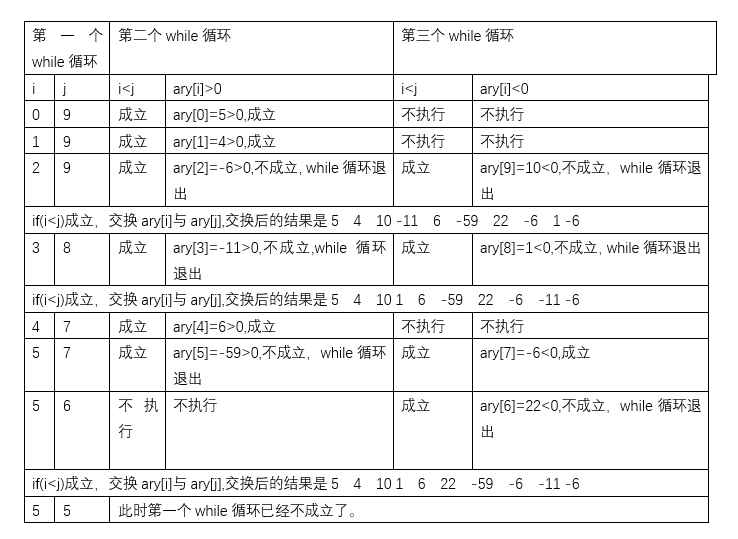
4.

#include<iostream>
#include<cstring>
using namespace std;
#define MAX 100
void solve(char first[], int spos_f, int epos_f, char mid[], int spos_m, int epos_m)
{
	int i, root_m;
	if(spos_f > epos_f)
		return;
	for(i = spos_m; i <= epos_m; i++)
		if(first[spos_f] == mid[i])
		{
			root_m = i;
			break;
		}
	solve(first, spos_f + 1, spos_f + (root_m - spos_m), mid, spos_m, root_m - 1);
	solve(first, spos_f + (root_m - spos_m) + 1, epos_f, mid, root_m + 1, epos_m);
	cout << first[spos_f];
}
int main()
{
	char first[MAX], mid[MAX];
	int len;
	cin >> len;
	cin >> first >> mid;
	solve(first, 0, len - 1, mid , 0, len - 1);	
	cout << endl;
	return 0;
}

输入：        7

ABDCEGF

BDAGECF

输出：__ DBGEFCA ____

【解析】非常复杂的一个函数递归调用（能看懂其中算法的话比较简单，手动模拟的失败率很高，没有找到简单的方法，目前就是通过模拟）

实际上是求树的后续遍历。

函数参数	first[]	spos_f	epos_f	mid[]	spos_m	epos_m
solve 1	first,	spos_f + 1	spos_f + (root_m – spos_m)	mid	spos_m	root_m – 1
solve 2	first	spos_f + (root_m – spos_m) + 1	epos_f,	mid,	root_m + 1	epos_m
	f	0	6	m	0	6
		1	2		0	1
		2	1		0	-1
		2	2		1	1
		3	2		1	0
		3	2		2	1

四．完善程序 (前4空，每空2.5分，后6空，每空3分，共28分)

1．（字符串替换）给定一个字符串S（S仅包含大小写字母），下面的程序将S中的每个字母用规定的字母替换，并输出S经过替换后的结果。程序的输入是两个字符串，第一个字符串是给定的字符串S，第二个字符串S’由26个字母组成，它是a-z的任一排列，大小写不定，S’规定了每个字母对应的替换字母：S’中的第一个字母是字母A和a的替换字母，即S中的A用该字母的大写替换，S中的a用该字母的小写替换；S’中的第二个字母是字母B和b的替换字母，即S中的B用该字母的大写替换，S中的b用该字母的小写替换；…… 以此类推。

#include <iostream>
#include <string.h>
char change[26], str[5000];
using namespace std;
void CheckChangeRule()
{
    int i;
    for (i = 0;i < 26;i ++)
    {
        if (  ①  )
               change[i] -= 'A' - 'a';  //
    }
}

void ChangeString()
{
    int i;
    for (i = 0;i <strlen(str);i ++)
    {
          if (  ②  )
                str[i] = change[str[i] - 'A'] -'a' + 'A'; 
          else
                 ③ 
    }
}
int main()
{
		int i;
cin >> str ;
    cin >> change;
    CheckChangeRule();
     ④
    cout << str << endl;
    return 0;

}

• ①change[i] >= ‘A’ && change[i] <= ‘Z'(只写change[i] <= ‘Z’也对) )
  【解析】根据上面函数的名字，可以猜想这个函数的目的是检查转换规则，下面的代码是 ‘A’是64，‘a‘是97，Change[i] -= -32 实际上就是 change[i] +=32 也就是将大写字母转换成小写字母，所以上面的if是检查是否是大写字母 。
  
• ②str[i] >= ‘A’ && str[i] <= ‘Z’（只写str[i] <= ‘Z’也对）
  【解析】根据下面的代码是将把无规律的ASCII码转换为字母对应的顺序(字母表顺序)（例如：设str[i]装的字符是A,则str[i]的值就为64，即64-64=0，变成了change[0]。），再由-‘a’+’A’得，str[i]=change[str[i]-‘A’]-32；（由题知，被替换的字母如果是大写字母，则替换字母也为大写字母）所以②处应该填判断大写字母
• ③str[i] = change[str[i] – ‘a’];
  【解析】如果为小写字母，则不需要转换
• ④ChangeString();
  【解析】main函数中少了一个函数调用，所以这里填写函数调用

---

---

2.(找第k大的数) 给定一个长度为1,000,000的无序正整数序列, 以及另一个数n (1<=n<=1000000), 然后以类似快速排序的方法找到序列中第n大的数（关于第n大的数：例如序列{1，2，3，4，5，6}中第3大的数是4）。

#include <iostream>
using namespace std;

int a[1000001],n,ans = -1;
void swap(int &a,int &b)  //交换两个数
{
	int c;
	c = a; a = b;	b = c;
}
int FindKth(int left, int right, int n)
{
	int tmp,value,i,j;
	if (left == right) return left;   
	tmp = rand()% (right - left) + left;  //tmp是基准
	swap(a[tmp],a[left]); //交换，让a[left] 成为基准
	value =  ① 
    
	i = left;
	j = right;
	while (i < j)
	{
		while (i < j &&  ② ) j --;
		if (i < j) {a[i] = a[j]; i++;} else break;
		while (i < j &&  ③ ) i ++;
		if (i < j) {a[j] = a[i]; j - -;} else break;
	}
        ④
	if (i < n) return  FindKth(  ⑤ );
		
	if (i > n) return   ⑥ 
	return i;
}
int main()
{
	int i;
	int m = 1000000;
	for (i = 1;i <= m;i ++)
		cin >> a[i];
	cin >> n;
	ans = FindKth(1,m,n);
	cout << a[ans];
    return 0;
}


---

• ①a[left];
  【解析】快排的思想，找一个基准，然后剩余的数跟基准比较，比基准大的往右放，比基准小的往左放，这里是用value作为基准
• ②a[j] < value (或a[j] <= value)
  【解析】快排思想，找到一个比基准大的数，并把它放到左侧，因为题目中说的是找第K大的数，所以是从大到小排列，比基准大的要放到左侧。
• ③a[i] > value （或a[i] >= value）
  【解析】找到一个比基准小的值，放到基准右侧
• ④a[i] = value;
  【解析】将value值赋值给a[i]
• ⑤i + 1,right,n
  【解析】递归调用，重新划分区间
• ⑥FindKth(left, i – 1, n);
  【解析】递归调用，重新划分区间

---

返回目录：NOPI/CSP信息学奥赛初赛

---